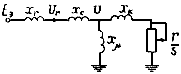
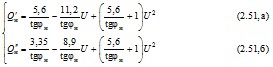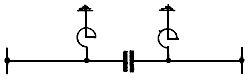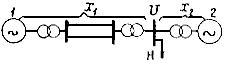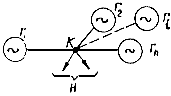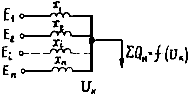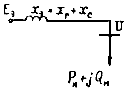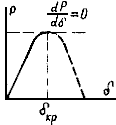РД 34.20.577
МИНИСТЕРСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ СССР
ГЛАВНОЕ ТЕХНИЧЕСКОЕ УПРАВЛЕНИЕ ПО ЭКСПЛУАТАЦИИ ЭНЕРГОСИСТЕМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ОПРЕДЕЛЕНИЮ УСТОЙЧИВОСТИ ЭНЕРГОСИСТЕМ
Часть 1
ПОДГОТОВЛЕНЫ ВНИИЭ, МЭИ, ВГПИиНИИ Энергосетьпроект, ЦДУ ЕЭС СССР, ИЭД АН УССР и НИИПТ: введение - ВНИИЭ, ЦДУ ЕЭС СССР, ИЭД; гл. 1 - ВНИИЭ, ЦДУ ЕЭС СССР; гл. 2 - МЭИ, Энергосетьпроект, ВНИИЭ; гл. 3 - МЭИ, Энергосетьпроект; гл. 4 - МЭИ, Энергосетьпроект; гл. 5 - ВНИИЭ, МЭИ; гл. 6 - ВНИИЭ, МЭИ; гл. 7 - ВНИИЭ, НИИПТ, ЦДУ ЕЭС СССР; гл. 8 - МЭИ; гл. 9 - ИЭД; гл. 10 - ВНИИЭ, ЦДУ ЕЭС СССР; приложения - ВНИИЭ, МЭИ, Энергосетьпроект, НИИПТ, ИЭД.
СОСТАВИТЕЛИ д-р техн. наук Л.Г. Мамиконянц (введение, гл. 1, 5-7, 10), канд. техн. наук Л.М. Горбунова (гл. 6), канд. техн. наук Ю.Е. Гуревич (гл. 6, приложения 1, 11, 12), инж. Л.Е. Либова (гл. 2), канд. техн. наук В.Ф. Тимченко (гл. 7), д-р техн. наук А.А. Хачатуров (гл. 5, 8, приложения 1, 8, 9), ВНИИЭ; д-р техн. наук В.А. Веников (гл. 2-6, 8, приложение 1), канд. техн. наук Н.Д. Анисимова (гл. 3, 8, приложения 3, 4, 14), д-р техн. наук Л.А. Жуков (гл. 2, 5), д-р техн. наук И.В. Литкенс (гл. 3, приложения 5, 6), канд. техн. наук В.А. Строев (гл. 3, 6, приложение 10), канд. техн. наук Д.А. Федоров (гл. 4, 5), канд. техн. наук А.Н. Цовьянов (гл. 4), МЭИ; д-р техн. наук Д.И. Азарьев (гл. 2-4), инж. Ю.В. Кишкин (гл. 2, приложения 2, 18) инж. Ю.В. Морошкин (гл. 3), инж. Ю.А. Поздняков (гл. 3, 4, приложение 7), канд. техн. наук З.Г. Хвощинская (гл. 2, приложение 18), инж. Л.П. Шипунова (гл. 2), Энергосетьпроект; д-р техн. наук С.А. Совалов (введение, гл. 1, 7, 10, приложение 1), канд. техн. наук М.Г. Портной (гл. 7, 10), ЦДУ ЕЭС СССР; д-р техн. наук Л.В. Цукерник (гл. 9, приложения 15, 16, 17) ИЭД; канд. техн. наук Е.А. Марченко (гл. 7, приложение 13), канд. техн. наук В.А. Андреюк (гл. 7, приложение 13), НИИПТ.
УТВЕРЖДЕНЫ заместителем начальника Главного технического управления по эксплуатации энергосистем К.М. Антиповым 24 марта 1977 г.
ВВЕДЕНИЕ
Настоящие Методические указания базируются на [Л.1] и имеют целью дать проектным, исследовательским и эксплуатирующим организациям рекомендации (но не обязательные предписания) по методам определения различных видов устойчивости энергосистем в целом и отдельных их элементов (межсистемных связей, нагрузки и др.), а также по принципиальному выбору мероприятий, необходимых для обеспечения устойчивости энергосистем.
Методические указания содержат общие, принципиальные рекомендации, а не детально разработанные методики. Последние при необходимости могут составляться применительно к конкретным условиям в зависимости от решаемых задач, имеющихся средств для анализа устойчивости энергосистем и т.п.
Как правило, рекомендации даются вариантно, т.е. предоставляется возможность выбрать один или несколько из известных и рекомендуемых к использованию методов анализа устойчивости энергосистем в зависимости от решаемой задачи, имеющихся исходных данных и средств анализа.
При описании отдельных методов отмечаются их основные положения, но детали и особенно выводы используемых формул не приводятся, однако даются ссылки на соответствующие литературные источники. Исключения составляют методы, еще не опубликованные или опубликованные в малотиражных изданиях.
В большей части случаев рекомендуемые методы анализа устойчивости энергосистем иллюстрируются примерами принципиального характера без детального изложения всего расчета.
В настоящее время многие вопросы теории и практики анализа и способов обеспечения устойчивости энергосистем находятся еще в стадии разработки. В частности, быстро развиваются и совершенствуются методы анализа устойчивости энергосистем с помощью электронных аналоговых и особенно цифровых вычислительных машин (ЦВМ). В связи с этим настоящие Методические указания содержат рекомендации по известным методам и не ограничивают опытное использование новых, не вошедших в них методов анализа устойчивости энергосистем и мероприятий по ее обеспечению.
В настоящие Методические указания включены и некоторые приближенные методы анализа и критерии устойчивости энергосистем и их нагрузок, теоретически недостаточно строго обоснованные, но проверенные на практике. Это, в частности, относится к упрощению схем энергосистем, к ряду практических критериев оценки устойчивости и т.п.
В данных Методических указаниях сохранены определения и термины, принятые в [Л.1] и приведенные также в приложении 1.
Методические указания состоят из десяти глав и ряда приложений.
В гл. 1 сформулированы задачи анализа устойчивости энергосистем на различных стадиях их проектирования и эксплуатации, даны определения видов их устойчивости, изложены общие рекомендации по анализу устойчивости: расчетные режимы, требуемая точность, анализ результатов, выбор средств для анализа и т.п. В гл. 2 даются указания по подготовке исходных данных и режимов, по преобразованию схем энергосистем (эквивалентированию).
В гл. 3, 4, 5 приведены рекомендации по анализу соответственно статической, динамической и результирующей устойчивости энергосистем. При этом, где необходимо, для каждого вида устойчивости даны рекомендации по специфическим особенностям применения специальных средств анализа (статических моделей, аналоговых и цифровых вычислительных машин).
Вопросам анализа устойчивости нагрузки посвящена гл. 6, при этом рассматриваются случаи, когда изменение режима нагрузки не может существенно повлиять на устойчивость параллельной работы генераторов энергосистемы, т.е. когда напряжение электросети, питающей нагрузку за некоторым сопротивлением, является заданным (не обязательно постоянным) и не зависящим от режима рассматриваемой нагрузки. Более сложный случай, в котором устойчивость собственно энергосистемы и питающейся от нее нагрузки взаимно сильно связаны, охватываются общими методами, приведенными в гл. 3, 4 и 5.
Специфические особенности анализа устойчивости энергосистем при наличии слабых межсистемных связей рассматриваются в гл. 7. Глава 8 посвящена основным вопросам анализа самовозбуждения (главным образом применительно к случаям наличия в их электросетях значительных емкостей) и самораскачивания (в общем случае учета активных сопротивлений всех элементов энергосистемы). Общие рекомендации по применению ЦВМ для анализа устойчивости энергосистем даны в гл. 9. Рекомендации по проведению натурных экспериментов в энергосистемах - в гл. 10. Главы 6-10 составляют содержание части 2 Методических указаний.
Изданные ранее "Основные положения и временные руководящие указания по определению устойчивости энергетических систем" будут в дальнейшем пересматриваться и дополняться на основе опыта их использования при проектировании и эксплуатации энергосистем и с учетом новых теоретических разработок. В соответствии с этим предполагается в будущем пересмотреть и дополнить настоящие Методические указания.
Глава 1. ОБЩИЕ УКАЗАНИЯ ПО ИССЛЕДОВАНИЮ УСТОЙЧИВОСТИ ЭНЕРГОСИСТЕМ
1.1. Основные требования к анализу устойчивости энергосистем
1.1.1. Расчеты устойчивости энергосистем должны выполняться в соответствии c [Л.1.].
1.1.2. Требуемая точность анализа устойчивости энергосистем зависит от конкретных решаемых задач, стадий проектирования и нужд эксплуатации, точности исходных данных и т.п.
1.1.3. Ориентировочные расчеты (расчеты на первых стадиях проектирования и перспективные эксплуатационные расчеты, выполняемые при выборе напряжений, количества цепей, принципиальных схем электропередачи и основных мероприятий, обеспечивающих осуществимость требуемых режимов с необходимым запасом) могут проводиться упрощенно в отношении схем и расчетных условий. Например, расчеты статической и динамической устойчивости заданного режима могут производиться при неизменных значениях ЭДС синхронных машин за их переходными сопротивлениями.
1.1.4. Уточняющие и настроечные расчеты при проектировании и в эксплуатации (выбор схем и рабочих режимов, уточнение параметров оборудования энергосистемы и определение запасов устойчивости в нормальных и послеаварийных режимах, уточнение требований к защите, системной автоматике, регуляторам возбуждения синхронных машин, определение параметров - уставок - этих устройств и т.п.) следует выполнять по достаточно полным схемам и с учетом основных факторов, которые могут оказать значительное влияние на результаты расчетов. Следует учитывать электромагнитные и электромеханические уравнения основных синхронных машин, статические и динамические характеристики нагрузок, характеристики регуляторов возбуждения, регуляторов первичных двигателей, фактические значения времени действия выключателей, уставки и характеристики устройств системной автоматики и релейной защиты и т.п.
Эти расчеты в условиях эксплуатации целесообразно сочетать с экспериментальными данными, полученными в энергосистеме (см. гл. 10).
1.1.5. Оперативно-эксплуатационные расчеты в зависимости от конкретных задач могут производиться весьма приближенно (грубая прикидка того или иного режима, показывающая наличие большего запаса, и т.п.) и с возможно более точным учетом конкретных условий и характеристик оборудования. В последнем случае целесообразно также использование результатов натурных испытаний.
1.1.6. Исследовательские расчеты также в зависимости от конкретных задач и стадий исследования могут производиться приближенно и возможно более точно, вплоть до представления машин и устройств системной автоматики наиболее полными системами уравнений. Последнее, в частности, оказывается необходимым при анализе влияния на устойчивость энергосистем параметров и характеристик самих машин и связанных с ними систем и устройств автоматики.
1.1.7. Анализ устойчивости энергосистем и выбор мероприятий для ее повышения следует производить с учетом конкретных задач для:
- режима нормальной работы энергосистемы при наиболее напряженных длительных условиях (максимальная активная или реактивная нагрузка энергосистемы, режимы наибольшей нагрузки основных линий электропередачи и других проверяемых элементов; утяжеленные условия питания проверяемых нагрузок для энергосистем с мощными гидроэлектростанциями - режимы паводка при минимальной нагрузке тепловых электростанций; для энергообъединений - режимы максимальных перетоков и т.п.);
- режимов, возникающих в результате отключения какого-либо основного элемента энергосистемы, вызывающих существенные ухудшения условий устойчивости и существующих до вмешательства персонала энергосистемы. Для таких режимов следует выполнять только расчеты статической устойчивости;
- ремонтных режимов, возникающих вследствие вывода в ремонт основных элементов энергосистемы, существенно влияющих на устойчивость энергосистемы в целом или проверяемого звена. При ориентировочных и уточняющих расчетах устойчивость этих режимов не проверяется, так как считается, что в этих режимах нагрузки линий электропередачи могут быть снижены до значений, достаточных для сохранения устойчивости. Однако устойчивость этих режимов должна, как правило, проверяться при выполнении оперативно-эксплуатационных расчетов;
- кратковременных особо тяжелых режимов, отличающихся от обычных меньшей надежностью и поэтому нормально не применяемых, а также для специальных случаев (например, для режимов работы синхронных машин с недовозбуждением).
Необходимость в проверке таких режимов может встретиться преимущественно в эксплуатационных условиях.
1.1.8. При ориентировочных расчетах, как правило, допустимо ограничиваться проверкой статической и динамической устойчивости, не производя проверки устойчивости нагрузки и результирующей устойчивости энергосистемы.
1.1.9. При уточняющих, настроечных и оперативно-эксплуатационных расчетах следует, как правило, анализировать все виды устойчивости собственно энергосистемы и узлов нагрузок.
1.1.10. В отдельных случаях, особенно при наличии продольной емкостной конденсации, необходима проверка возможности нарушения статической устойчивости энергосистемы или узлов нагрузки (в состав которых входят синхронные двигатели) вследствие самораскачивания, вызванного в режиме малых нагрузок относительно большим активным сопротивлением. При наличии значительных продольных или поперечных емкостей необходима также проверка на отсутствие самовозбуждения.
1.2. Методы анализа устойчивости энергосистем
1.2.1. Методом аналогий (подобия) следует пользоваться в ориентировочных расчетах, если простым пересчетом параметров на основе соотношений подобия [Л.2] можно свести рассматриваемую задачу к другой, уже имеющей оценку устойчивости на основе данных эксплуатации или по ранее выполненным исследованиям (расчетам, испытаниям и т.п.).
1.2.2. Применение относительно простых критериев устойчивости позволяет решать следующие задачи: определение статической устойчивости по "сползанию" с использованием критерия равенства нулю свободного члена характеристического уравнения системы или эквивалентных ему практических критериев, в которых используются производные передаваемой активной мощности по углу, реактивной мощности по напряжению и т.п.; определение динамической устойчивости по методу площадей; определение результирующей устойчивости по критериям ресинхронизации без выявления характера процесса; проверка отсутствия самовозбуждения по простейшим критериям, определяющим соотношения между индуктивными, емкостными и активными сопротивлениями, при которых это явление не возникает.
1.2.3. Уточненные методы анализа устойчивости энергосистем предназначены для большей части задач. Они основаны на анализе линеаризованных (для статической устойчивости) и нелинейных (для динамической и результирующей устойчивости) уравнений.
Для исследования статической устойчивости используются строгие критерии (Гурвица, Рауса, Михайлова, метод D-разбиения), дающие необходимые и достаточные условия устойчивости. Степень упрощения элементов сложной энергосистемы может быть разной (различное количество электростанций, для которых не учитываются электромагнитные переходные процессы в контурах ротора и которые представляются упрощенно в виде постоянной ЭДС за постоянным сопротивлением, разное представление нагрузок и т.д.).
1.3. Средства анализа устойчивости энергосистем
1.3.1. Исследования устойчивости энергосистем могут выполняться с помощью разных средств, однако возможности каждого из них разные и поэтому различны области их применения. Средства непрерывно развиваются и совершенствуются, новые средства вытесняют менее совершенные. В Методических указаниях дается лишь краткая характеристика средств, используемых в настоящее время для исследования устойчивости энергосистем.
1.3.2. Простейшие средства, позволяющие выполнять расчеты вручную (логарифмическая линейка, арифмометр, клавишная вычислительная машина), следует использовать только при оценке устойчивости энергосистем с помощью методов аналогий, практических критериев и в упрощенных расчетах простых схем.
1.3.3. Аналоговые вычислительные машины (АВМ), предназначенные для решения систем нелинейных дифференциальных уравнений, целесообразны и используются для исследований устойчивости энергосистем, содержащих лишь небольшое количество индивидуально учитываемых электростанций (до трех-четырех), работающих в несложной электросети, так как с усложнением схемы трудности ее математического моделирования резко возрастают. Аналоговые вычислительные машины эффективны для исследования влияния на устойчивость различных средств автоматики и для выбора их характеристик.
Удобством использования АВМ, работающих в соответствии с методами математического моделирования [Л.3], является относительная легкость вариации параметров и характеристик моделируемого оборудования (в том числе с учетом нелинейностей), возможность быстрого получения наглядных результатов. Путем создания сравнительно простых преобразовательных переходных блоков имеется возможность сочетания АВМ с реальными устройствами автоматики.
1.3.4. Статические модели энергосистем, которые долгое время были единственным средством анализа устойчивости сложных энергосистем, еще могут использоваться для расчетов установившихся режимов и анализа апериодической статической устойчивости энергосистем с использованием практических критериев и динамической устойчивости методом последовательных интервалов.
Статические модели содержат активные и реактивные сопротивления, воспроизводящие пассивные элементы схемы замещения электрической системы, и устройства, позволяющие изменять вручную фазу и значения напряжений, подводимых к этой схеме, и таким образом воспроизводить режим работы электростанций.
Статические модели просты и надежны в эксплуатации, однако производительность работы на таких моделях относительно невелика. В настоящее время они вытесняются автоматическими моделями, производительность которых во много раз выше.
1.3.5. Автоматические модели электрических систем [Л.4] могут быть использованы для исследования любых видов устойчивости, однако наиболее эффективны они при исследованиях установившихся режимов и динамической устойчивости.
В отличие от статических моделей в автоматических моделях электрических систем, разработанных в Энергосетьпроекте, синхронные машины и асинхронные двигатели представлены специальными электромеханическими устройствами - генераторными станциями и нагрузками, автоматически воспроизводящими установившиеся режимы, электромеханические переходные процессы синхронных машин и динамические характеристики потребителей энергии. Управление коммутационными переключениями осуществляется программным блоком, а регистрация фаз ЭДС - с помощью автоматического потенциометра (самописца). Предусмотрено также применение цифровой регистрации. Переходный процесс воспроизводится в замедленном масштабе времени (1:100), причем этот процесс в любой момент может быть остановлен на любое время и вновь продолжен без искажения результатов. Такие модели могут содержать большое количество станций и нагрузок, причем увеличение их числа не увеличивает времени воспроизведения электромеханического переходного процесса, возрастает лишь время набора схемы и установки режима.
Модели с использованием лишь электронных элементов (типа "Дельта", разработка ВНИИЭ) могут быть использованы для исследования любых видов устойчивости энергосистем, в том числе и для исследований, связанных с асинхронным ходом синхронных машин. Такие модели могут работать в натуральном и ускоренном масштабе времени. Имеются принципиальные возможности непосредственного сочетания модели генераторов с натурными устройствами систем автоматического регулирования и защиты, если рабочая частота модели соответствует рабочей частоте устройств.
Для исследований установившихся режимов и динамической устойчивости энергосистем средней сложности могут также использоваться автоматические модели последовательного действия, разработанные АрмНИИЭ. Основной особенностью этих моделей, отличающих их от описанных, является наличие лишь одного вычислительного устройства, автоматически подключаемого поочередно к элементам и изменяющего фазу и значение напряжения, подводимого к исследуемой схеме в точках, куда подключены синхронные машины, и лишь одного вычислительного устройства, подключаемого к элементам, воспроизводящим нагрузку. Эти вычислительные устройства выполняют роль оператора в статических моделях. Процесс расчета на них аналогичен: при установке режима используется итеративный метод, а при расчете переходного процесса - метод последовательных интервалов. Время расчета на таких моделях увеличивается соответственно увеличению количества станций.
1.3.6. Цифровые вычислительные машины следует рассматривать как наиболее эффективные и перспективные средства анализа устойчивости энергосистем с требуемой для многих проектных, эксплуатационных и исследовательских задач высокой степенью полноты и точности математического описания системы в целом (учет большого количества машин, сложной сети и т.п.), отдельных ее элементов и систем автоматики. Цифровые вычислительные машины и методы анализа устойчивости, выполняемые с их помощью, быстро совершенствуются (см. гл. 9).
1.3.7. Физические (электродинамические) модели энергосистем следует применять главным образом для проверки вновь разрабатываемых устройств управления, регулирования и защиты в условиях, близких к тем, которые имеют место в реальных энергосистемах.
Физические модели энергосистем [Л.5] представляют собой лабораторные физические модели генераторов, трансформаторов, линий и других элементов энергосистем, специально разработанные на основе теории подобия. Эти модели допускают изменение параметров в диапазонах, соответствующих реально имеющимся в энергосистемах. Такие модели проще, чем математические, сочетаются с натурными устройствами автоматики и защиты. Они могут работать в комплексе с аналоговыми математическими моделями тех процессов или устройств, физическое моделирование которых затруднительно или нецелесообразно (например, с математическими моделями турбины и ее системы управления).
Физические модели существенно уступают математическим в гибкости и оперативности, но позволяют проводить исследования с учетом ряда факторов, математическое описание которых затруднено или еще отсутствует (например, сложные несимметрии в системе с несколькими генераторными станциями).
1.4. Выбор методов и средств анализа устойчивости энергосистем
1.4.1. Выбор методов и средств анализа устойчивости энергосистем должен производиться с учетом конкретных задач, категорий расчетов и имеющихся возможностей.
1.4.2. Принципиально следует начинать оценку устойчивости энергосистем с более простых методов и применять более сложные, если возможные погрешности результатов, полученных простым методом, больше допустимых для решаемой задачи (например, если полученный запас по устойчивости соизмерим с величиной погрешности метода). Если коэффициенты запаса, полученные по методу аналогий, по практическим критериям устойчивости или в результате расчетов упрощенных схем, значительно превышают нормативные коэффициенты и возможные погрешности метода и исходных данных, то проверку устойчивости более точными методами можно не производить, за исключением случаев, когда это диктуется необходимостью более детального анализа процессов, возможных путей улучшения технико-экономических показателей системы за счет снижения излишних запасов, уточнения параметров и характеристик средств автоматики и защиты.
1.4.3. Более точные методы (расчеты, эксперименты на моделях и в энергосистемах) необходимы в большинстве случаев уточняющих, настроечных, оперативно-эксплуатационных и исследовательских категорий расчетов.
1.4.4. Важнейшее значение для окончательного суждения об устойчивости конкретных энергосистем, а также о различных мероприятиях, направленных на ее повышение, имеет сочетание расчетов с натурными экспериментами в энергосистемах.
1.4.5. Следует учитывать, что все методы анализа устойчивости энергосистем дают приближенные результаты из-за погрешностей самого метода, неточности исходной информации о параметрах и режимах работы энергосистем, а также из-за вероятностного характера как параметров самого исходного режима, так и параметров возмущения (например, места КЗ, его продолжительности и т.п.).
При получении результатов, близких по устойчивости к предельно допустимым (с учетом нормативных коэффициентов запаса), нельзя выносить окончательных суждений о допустимости того или иного режима, о необходимости применения специальных мероприятий для повышения устойчивости, об оптимальной настройке устройств автоматики и защиты только по результатам одного расчета. Для получения более достоверных результатов анализа устойчивости энергосистем в таких случаях следует хотя бы приближенно оценить вероятность возникновения условий, принятых в расчете, в частности возможные пределы изменений исходных режимов, параметров и характеристик системы и нагрузок, и выполнить для них серию расчетов для определения влияния на устойчивость вариаций указанных условий.
1.4.6. Все расчеты устойчивости долины выполняться с учетом действия основных средств для ее повышения [Л.6-19].
Следует также учитывать:
- вероятность возникновения тех или иных причин нарушения устойчивости (режимов и возмущений);
- последствия нарушения синхронизма, возможность и допустимость асинхронного хода с последующей ресинхронизацией;
- эффективность рассматриваемых средств повышения устойчивости*.
_____________
* В настоящих Методических указаниях методика технико-экономических расчетов для выбора целесообразных способов и средств повышения устойчивости не рассматривается. Может быть использован метод, основанный на определении приведенных народнохозяйственных, затрат для вариантов, отличающихся средствами повышения устойчивости.
Глава 2. ПОДГОТОВКА ИСХОДНЫХ ДАННЫХ, СХЕМ И РЕЖИМОВ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ ЭНЕРГОСИСТЕМ. УПРОЩЕНИЕ СХЕМ (ЭКВИВАЛЕНТИРОВАНИЕ)
2.1. Расчетные параметры элементов электрических систем
2.1.1. Расчеты переходных процессов, а также исходных установившихся режимов выполняются применительно к схемам замещения (расчетным схемам). Расчетная схема электрической системы составляется из схем замещения отдельных элементов системы, связанных друг с другом так же, как соединены соответствующие элементы в рассматриваемой системе [Л.20, 21].
В схемы замещения электрических систем могут входить в отдельных случаях также элементы, представляющие собой схемы предварительно преобразованных участков системы. Эти элементы, являющиеся обобщенными схемами таких преобразованных участков, представляют собой в общем случае многоугольники с диагоналями и нагрузочными сопротивлениями в вершинах.
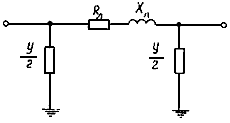
2.1.2. Линии электропередачи в общем случае представляются П-образными схемами замещения (рис. 2.1) с учетом активного Rл и реактивного хл сопротивления линии и реактивной (емкостной) проводимости Yл линии электропередачи на землю.
Рис. 2.1. Схема замещения линии электропередачи
2.1.3. Для определения параметров этих схем исходными данными являются:
- номинальное напряжение линии;
- длина линии;
- количество цепей линий;
- марка и сечение провода;
- расположение проводов на опоре и расстояние между проводами;
- наличие троса и его марка.
2.1.4. Сопротивления схем замещения линии определяются по формулам
= Rл + jxл; хл = kXx0l;
(2.1)
Rл = kRr0l; Yл = kYb0l,
где kR, kX, kY - поправочные коэффициенты, учитывающие влияние равномерного распределения параметров линии вдоль ее длины;
x0 - погонное значение индуктивного сопротивления линии, Ом/км;
l - длина линии, км;
r0 - погонное значение активного сопротивления линии, Ом/км;
b0 - погонное значение емкостной проводимости линии, См/км.
При длине линии электропередачи до 300 км поправочные коэффициенты принимаются равными 1; при длине 300-1000 км они определяются по формулам
;
;
. (2.2)
При длине линий электропередачи более 700-1000 км параметры схемы замещения определяются с учетом комплексных поправочных коэффициентов (;
) по формулам
;
, (2.3)
где - погонное значение комплексного сопротивления линии;
- погонное значение комплексной проводимости линии.
,
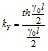
где - коэффициент распространения волны.
2.1.5. Погонное значение активного сопротивления в приведенных формулах определяется по справочной таблице приложения к ГОСТ 839-59 на провода или приближенно по формуле
, (2.5)
где kскр - коэффициент скрутки (обычно принимается 1,02-1,03);
ρ - удельное сопротивление материала провода (при t =20 °С), для меди ρ = 17,9; для алюминия ρ = 29,5
;
F- фактическое сечение проводящей части провода в фазе, мм2.
Погонное индуктивное сопротивление линии (x0) определяется по формуле
, (2.6)
где - среднегеометрическое расстояние между проводами (или центрами фаз при расщепленных проводах), мм;
D12, D23, D31 - расстояние между проводами на опоре, мм;
Rэ - эквивалентный радиус провода, мм;
n - число проводов в фазе.
При нерасщепленных проводах значение Rэ равно радиусу провода R. Эквивалентный радиус Rэ в зависимости от числа расщепленных проводов внешним диаметром d в фазе при расположении их в вершинах правильного m-угольника со стороной a определяется по формулам
n | 2 | 3 | 4 |
Rэ |
Реактивная (емкостная) проводимость 1 км фазы линии b0 с нерасщепленными проводами (См/км) при частоте 50 Гц определяется по формуле
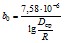
2.1.6. Емкость C (мкФ) одной цепи линии длиной l (км) при любом расположении проводов на опоре определяется по формуле
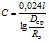
Для линии с расщепленными фазами емкость определяется по аналогичной формуле
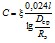
где ξ - коэффициент, учитывающий влияние земли, тросов и более точного распределения зарядов на емкость линии.
Для линии электропередачи напряжением 500 кВ с двумя тросами и горизонтальным расположением проводов ξ =1,05, поэтому в этом случае
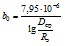
При известной емкостной проводимости емкость, соответствующая П-образной схеме замещения линии, определяется по формуле
СН = СК = , (2.11)
где СН = СК - емкости в начале и конце линии, Ф;
n - число параллельных цепей;
ω - угловая частота, ω = 314 с-1.
2.1.7. При упрощенных расчетах активное сопротивление линии принимается равным нулю. В этих же случаях емкость линии с номинальным напряжением 110 кВ и ниже, а также для коротких линий с напряжением 150 и 220 кВ не учитывается. При изучении переходных процессов в системах, имеющих малую мощность или содержащих кабельные линии, активные сопротивления и емкость кабельных линий должны учитываться.
2.1.8. Активное и реактивное сопротивления линии для системы токов обратной последовательности имеют те же значения, что и соответствующие сопротивления прямой последовательности.
Активное сопротивление (Ом/км) фазы одноцепной трехфазной линии для системы токов нулевой последовательности r0(0) определяется по формуле
r0(0) ≈ r0 + 0,15, (2.12)
где r0 - активное сопротивление провода для системы токов прямой последовательности.
Для одной фазы двухцепной трехфазной линии
r0(0) ≈ 0,5r0 + 0,15. (2.13)
Реактивное сопротивление нулевой последовательности линии x0(0) при известном сопротивлении прямой последовательности x0 ориентировочно определяется с помощью табл. 2.1.
Таблица 2.1
Характеристика линии | |
Одноцепная линия: | |
без тросов | 3,5 |
со стальными тросами | 3,0 |
с хорошо проводящими тросами | 2,0 |
Двухцепная линия: | |
без тросов | 5,5 |
со стальными тросами | 4,7 |
с хорошо проводящими тросами | 3,0 |
Емкостная проводимость нулевой последовательности, учитываемая обычно для линий напряжением 500 кВ и выше, составляет 0,6-0,7 соответствующей проводимости прямой последовательности.
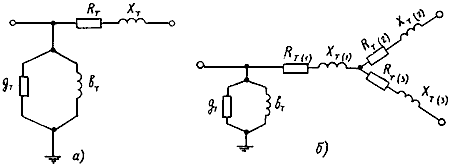
2.1.9. Трансформаторы и автотрансформаторы. При составлении схемы замещения электрической системы двухобмоточные трансформаторы представляются Г-образными схемами (рис. 2.2, а), трехобмоточные трансформаторы, а также автотрансформаторы - схемами в виде трехлучевой звезды (рис. 2.2, б), к одному из лучей которой подсоединяется ветвь намагничивания. В общем случае ветвь намагничивания удобно относить к стороне высшего напряжения и объединять с ветвью емкостной проводимости схемы замещения линии, связанной с трансформатором.
Рис. 2.2. Схемы замещения трансформаторов:
а - двухобмоточного; б - трехобмоточного
2.1.10. Исходными данными для определения параметров схем замещения трансформаторов являются:
- номинальная мощность;
- номинальные напряжения с указанием рабочих ответвлений трансформаторов;
- потери КЗ;
- потери холостого хода;
- ток намагничивания;
- реактивные сопротивления или напряжения КЗ трансформаторов (для трехобмоточных трансформаторов должны быть даны индивидуальные или междуобмоточные реактивные сопротивления для всех трех обмоток) в процентах или относительных единицах;
- схемы соединений обмоток трансформаторов с указанием заземленных нулевых точек.
2.1.11. Параметры схемы замещения двухобмоточных трансформаторов определяются по следующим формулам. Реактивное сопротивление (Ом)
, (2.14)
активное сопротивление (Ом)
(2.15)
или
, (2.16)
активная проводимость (См)
; (2.17)
реактивная проводимость (См)
, (2.18)
где Uном - номинальное междуфазное напряжение трансформатора, кВ;
Sном - номинальная мощность трехфазного трансформатора или трехфазной группы однофазных трансформаторов, МВ·А;
UК, UR - соответственно реактивная и активная составляющие напряжения КЗ трансформатора, % номинального напряжения;
ΔPкз - потери КЗ (потери в меди) трех фаз трансформатора, кВт;
ΔPхх - потери холостого хода (потери в стали) трех фаз трансформатора, кВт;
Iхх- ток холостого хода трансформатора, % номинального тока.
2.1.12. Для трехобмоточных трансформаторов и автотрансформаторов индуктивные сопротивления Хт(1); Хт(2); Хт(3) трехлучевой схемы замещения определяются по формулам
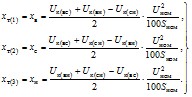
Индексы в, с, н обозначают соответственно величины на стороне высокого, среднего и низкого напряжений.
Если значения напряжений КЗ указаны отнесенными к типовой мощности трансформатора Sтип(,
)*, то
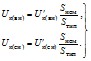
_____________
* Для некоторых типов автотрансформаторов напряжения и
указываются отнесенными к мощности обмотки низшего напряжения Sнн ≠ Sтип. В этом случае в указанные ниже формулы вместо Sтип подставляется Sнн.
2.1.13. Активные сопротивления в схеме замещения трехобмоточных трансформаторов и автотрансформаторов определяются следующим образом. В случае если известны все три значения потерь КЗ между парами обмоток, то они сначала приводятся к номинальной мощности, так как завод-изготовитель сообщает, как правило, эти значения () отнесенными к мощности S меньшей обмотки трансформатора или к типовой мощности автотрансформатора
. (2.21)
После этого определяются
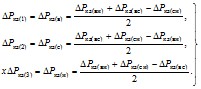
и активные сопротивления, например:
. (2.23)
В случае если в каталожных данных указывается только значение максимальных потерь КЗ, то активные сопротивления трехобмоточных трансформаторов определяются следующим образом:
- при равных мощностях обмоток
; (2.24)
- для обмотки, мощность которой составляет 66,7% мощностей остальных двух обмоток,
Rт66,7% = 1,5Rт100%; (2.25)
- при двух обмотках, выполненных на мощность 66,7% мощности третьей обмотки,
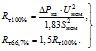
2.1.14. При приближенных расчетах активные сопротивления и активные проводимости ветви намагничивания трансформаторов и автотрансформаторов могут не учитываться, если предметом исследования не являются переходные процессы в режимах малых нагрузок.
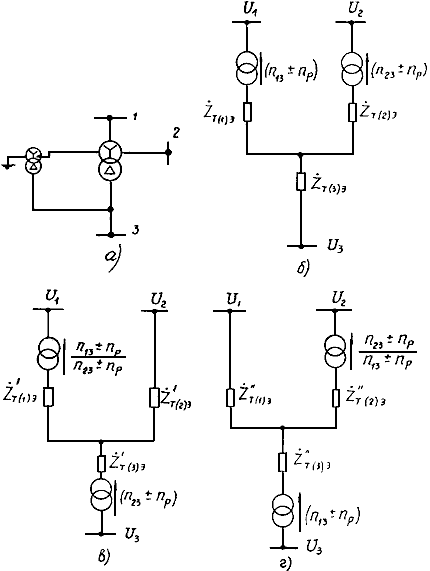
2.1.15. При наличии вольтодобавочных трансформаторов, включенных в нейтраль автотрансформатора (рис. 2.3, а), схема замещения составляется, как показано на рис. 2.3, б, в, г. Сопротивления схемы замещения в этом случае определяются по формулам
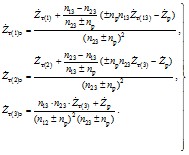
где ,
,
- сопротивления ветвей высшего, среднего и низшего напряжений эквивалентной схемы замещения с учетом добавочного трансформатора, приведенные к ступени напряженияU3;
,
,
- сопротивления обмоток высшего, среднего и низшего напряжений автотрансформатора, приведенные каждое к своему напряжению;
- сопротивление добавочного трансформатора;
n12, n13, n23 - соответствующие номинальные коэффициенты трансформации автотрансформатора;
;
;
; (2.28)
- коэффициент трансформации добавочного трансформатора при данном ответвлении.
Рис. 2.3. Схемы автотрансформатора при наличии вольтодобавочного трансформатора в нейтрали:
а - принципиальная схема; б - эквивалентная схема, приведенная к ступени U3;
в - эквивалентная схема, приведенная к ступени U2; г - эквивалентная схема, приведенная к ступени U1
Представленная на рис. 2.3, б расчетная схема соответствует положительному регулированию и знаку плюс в вышеприведенных формулах.
2.1.16. Приведение к другой ступени напряжения осуществляется простым пересчетом сопротивлений. При приведении к ступени напряжения U2 получаем (см. рис. 2.2, в):
,
, (2.29)
.
При приведении к ступени напряжения U1 получаем (см. рис. 2.3, г):
,
, (2.30)
.
2.1.17. Сопротивления схемы замещения нулевой последовательности трансформаторов и автотрансформаторов в значительной мере определяются их конструкцией и схемой соединения. Они могут быть определены согласно [Л.9, рис. 13.6 и 13.7].
2.1.18. Выбор систем уравнений для генераторов, компенсаторов и синхронных двигателей следует проводить с учетом целей расчета, требований к точности результатов и влияния данной синхронной машины на исследуемый процесс.
2.1.19. Контроль погрешностей, обусловленных допущениями, принятыми в уравнениях машины, в общем случае следует осуществлять заменой этих уравнений более точными.
2.1.20. В расчетах устойчивости генераторов, работающих в сложных энергосистемах, для тех синхронных машин, переходные процессы в которых оказывают существенное влияние на результаты расчетов, следует использовать упрощенные уравнения Парка-Горева, которые во взаимной системе относительных единиц [Л.3] имеют вид
-Ψq = ud; (2.31, а)
Ψd = uq; (2.31, б)
PΨf + rfif = uf ; (2.31, в)
pΨ1d + r1di1d = 0; (2.31, г)
pΨ1q + r1qi1q = 0; (2.31, д)
ωcτjps + Ψdiq - Ψqid = Mт, (2.31, е)
где d, q - индексы, указывающие, на какую ось (поперечную или продольную) спроектированы соответствующие векторы;
Ψd, Ψq - потокосцепления статора;
Ψf - потокосцепление обмотки возбуждения;
Ψ1d, Ψ1q - потокосцепления демпферных контуров в поперечной и продольной оси;
id, iq, if, i1d, i1q - токи статора, обмотки возбуждения и демпферных контуров;
rf, r1d, r1q- активные сопротивления;
Uf - напряжение на кольцах ротора;
Mт - момент турбины;
τj- механическая постоянная инерции агрегата в целом;
ωc - синхронная скорость;
p - оператор дифференцирования;
s - скольжение по отношение к синхронной оси;
δ - угол между осью q и вектором U, имеющим проекции Ud и Uq.
Уравнения (2.31, а)-(2.31, е) дополняются системой уравнений для потокосцеплений
Ψd = xdid + xad(if + i1d); (2.32, а)
Ψq = xqiq + xaqi1q; (2.32, б)
Ψf = xfif + xad(id + i1d); (2.32, в)
Ψ1d = x1di1d + xad(id+ if); (2.32, г)
Ψ1q = x1qi1q + xaqiq. (2.32, д)
2.1.21. Полные уравнения Парка-Горева [Л.3, 11] следует применять в расчетах, когда требуется учет апериодических составляющих токов статора [Л.22, 23] .
2.1.22. В расчетах динамической (но не результирующей) устойчивости иногда возможен отказ от учета демпферных контуров. Тогда синхронная машина описывается системой уравнений
-Ψq = ud,
Ψd = uq,
PΨf + rfif = uf,
Ψd = xdid + xadif, (2.33)
Ψq = xqiq,
Ψf = xfif + xadid,
ωcτjps + Ψdiq - Ψqid = Mт.
Применяются различные формы записи этих уравнений (см. аналогичные уравнения Лебедева-Жданова-Лонглея в гл. 4).
При использовании уравнений (2.33) влияние демпферных контуров может быть приближенно учтено введением соответствующим образом подобранного демпферного коэффициента kд в уравнение движения
ωcτjps + kдs + Ψdiq - Ψqid = Mт. (2.34)
2.1.23. Для синхронных машин, электромагнитные переходные процессы в которых не влияют на результаты расчетов, в расчетах динамической устойчивости (первого цикла качаний) и статической устойчивости (в условиях, обеспечивающих отсутствие самораскачивания) допустимо принимать = const или
= const;
эта ЭДС включается за сопротивлением.
2.1.24. В схемах замещения обратной последовательности генераторы представляются их реактивными сопротивлениями обратной последовательности x2, причем ЭДС за ними считаются равными нулю.
2.1.25. Синхронные генераторы, синхронные двигатели и компенсаторы характеризуются следующими основными параметрами:
- номинальной мощностью;
- номинальным коэффициентом мощности cosφном;
- номинальным напряжением;
- реактивными сопротивлениями xd, ,
, xq,
, x2, x0 в относительных единицах;
- постоянной инерции агрегата (генератор + турбина)τj, с, или маховым моментом GD2, т⋅м2;
- синхронным числом оборотов n, об/мин;
- постоянной времени обмотки возбуждения при разомкнутом статоре, с.
Дополнительные параметры, необходимые при моделировании генератора схемами для продольной и поперечной оси машины, определяются по каталогам, на основании экспериментов или рассчитываются в соответствии с методиками, изложенными в [Л.3].
2.1.26. Сопротивления генераторов в абсолютных единицах по каталожным данным вычисляются по формуле
, (2.35)
где x - в относительных единицах;
Sном - номинальная кажущаяся мощность, МВ⋅А;
Uном - номинальное напряжение, кВ.
В эту формулу подставляется номинальное напряжение той ступени трансформации, к которой относится вычисляемое сопротивление.
При известном маховом моменте механическая постоянная инерция агрегата τj определяется по формуле
, (2.36)
где GD2 - суммарный маховой момент электрической машины и турбины (или приводимого механизма), т⋅м2;
n - синхронное число оборотов, об/мин*.
_____________
* В уравнении движения (2.31, е), записанном в относительных единицах, часто применяют широко распространенное допущение - замену электромагнитного момента (Ψdiq - Ψqid) мощностью. Соответственно механический момент также заменяют мощностью.
2.1.27. Нагрузку в схемах замещения электрических систем в зависимости от цели расчетов, требований к их точности и располагаемых средств вычислительной техники следует представлять различными способами:
- постоянными мощностями Pн + jQн в расчетах нормальных режимов с уровнями напряжения, близкими к номинальным;
- постоянными сопротивлениями или проводимостями
в упрощенных расчетах статической устойчивости или переходных процессов (динамической устойчивости); в последнем случае должна быть уверенность в том, что устойчивость нагрузки (см. гл. 6) не нарушается при рассматриваемом возмущении или нарушение ее устойчивости не оказывает существенного влияния на результаты расчетов;
- статическими характеристиками Рн = f1(U), Qн = f2(U)* в расчетах устойчивости главным образом для правильной оценки устойчивости системы и нагрузки в послеаварийном режиме;
_____________
* Статические характеристики нагрузки по частоте Рн = φ1(f), Qн = φ2(f), используются в расчетах, где исследуются процессы понижения частоты в дефицитных районах после их отделения от энергосистемы. При этом учитывается действие АЧР.
- динамическими характеристиками Рн = f1(U1t), Qн = f2(U1t).
Эти характеристики могут быть заложены в расчет как исходные данные, если они известны (например, по экспериментам в системе), для выбранных возмущений. Обычно же такие характеристики определяются в ходе самого расчета, в который вводятся уравнения, отражающие главные виды потребителей (основной из них - асинхронные двигатели), поэтому в данном случае говорят о представлении комплексной нагрузки по ее составу.
2.1.28. Значение сопротивления определяется по заданной мощности нагрузки и напряжению в узле, через который она включается в схему. В тех случаях, когда схема замещения составляется при неизвестных напряжениях в узлах, определение сопротивления нагрузки ведется по номинальному или среднему напряжению.
Для аналитических расчетов целесообразно принимать схему замещения нагрузки в виде последовательно соединенных активного rн и реактивного хн сопротивлений, причем
, (2.37)
где cosφн - коэффициент мощности нагрузки;
Sн - кажущаяся рабочая мощность нагрузки*.
_____________
* Везде принимается, что .
При использовании моделей переменного тока более удобно нагрузку представлять параллельно соединенными активными и реактивными сопротивлениями, равными
;
. (2.38)
В схемах обратной последовательности значения сопротивлений нагрузки (отн.ед.) следует принимать равными:
а) при номинальном напряжении 6-10 кВ
= 0,08 + j0,24; (2.39)
б) при номинальном напряжении 110 кВ
= 0,09 + j0,36; (2.40)
За базисные величины при вычислении этих сопротивлений следует принимать номинальное напряжение питающей сети и кажущуюся рабочую мощность нагрузки Sн.
2.1.29. В схемах нулевой последовательности сопротивление нагрузки определяется в соответствии с реальной схемой ее питания. При отсутствии конкретных данных по схеме питания для расчетов при удаленных от нагрузки повреждениях или для определения шунтов короткого замыкания допустимо сопротивление нулевой последовательности нагрузки принимать j0,12 отн.ед. при базисных условиях, указанных выше.
2.1.30. Статические характеристики нагрузки по напряжению [Л.24-31] могут быть заданы на основании натурного эксперимента, расчета с детальным учетом состава нагрузки (причем для характеристик реактивной нагрузки особо важную роль играет учет зависимости потерь холостого хода трансформаторов Qμ от напряжения) или на основании статистических данных.
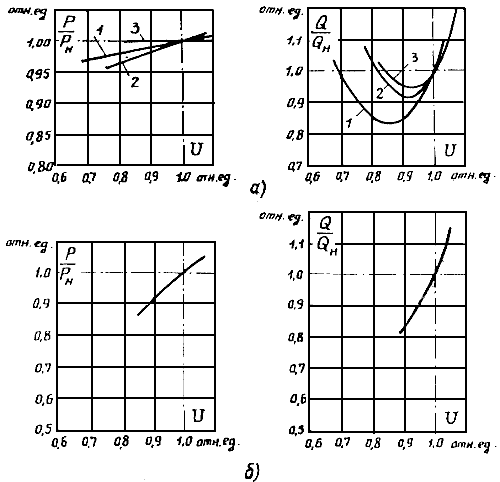
Примеры статических характеристик нагрузки, полученных в результате экспериментов в системах, приведены на рис. 2.4.
Рис. 2.4. Примеры статических характеристик нагрузки (по экспериментальным данным):
а - промышленная нагрузка (узлы: 1, 2, 3); б - городская нагрузка
2.1.31. Статические характеристики по напряжению (при номинальной частоте) основных элементов нагрузки:
а) асинхронные двигатели
P ≈ const; (2.41)
, (2.42)
где хко - сопротивление короткого замыкания двигателя при скольжениях, близких к нулю;
kз - коэффициент загрузки;
xμ- сопротивление шунта намагничивания;
б) синхронные двигатели (без учета явнополюсности)
P ≈ const;
, (2.43)
где
;
для всех элементов нагрузки принимается, что Q > 0 при потреблении реактивной мощности из сети;
в) осветительная нагрузка (лампы накаливания)
P ≈ gU1,6; (2.44)
г) бытовая нагрузка
P ≈ gU2; Q ≈ bU2; cosφ ≈ 0,95; (2.45)
д) печи сопротивления
P ≈ gU2; Q ≈ 0; (2.46)
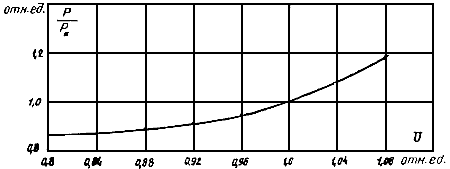
е) карборундовые печи - см. примерные характеристики на рис .2.5;
ж) дуговые печи - см. примерные характеристики на рис. 2.6;
з) индукционные печи - замещаются постоянными активными и индуктивными сопротивлениями;
и) тяговую нагрузку в первом приближении можно заменить постоянными активными и реактивными сопротивлениями;
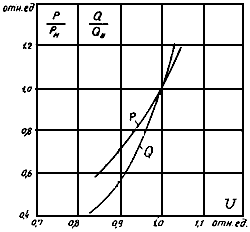
к) для электролизной установки примерные статические характеристики приведены на рис. 2.7;
л) потери холостого хода Q в трансформаторах (ориентировочно)
Q ≈ Qμт(0,4 + 0,6U11), (2.47)
где потери при номинальном напряжении Qμт могут быть приняты в размере до 8% от значения Sном.т для низковольтных трансформаторов (их средняя загрузка близка к 30%) и 3% или менее для высоковольтных трансформаторов. Напряжение U в (2.47) - в относительных единицах;
м) батареи конденсаторов
Q = -QcU2, (2.48)
где значение Qc целесообразно подбирать так, чтобы сумма реактивных мощностей всех элементов нагрузки соответствовала реальному значению коэффициента мощности в узле нагрузки.
Рис. 2.5. Статистические характеристики карборундовой печи
Рис. 2.6. Статистическая характеристика дуговой печи
Рис. 2.7. Статистические характеристики электролизной установки (с учетом ртутных преобразователей)
2.1.32. При расчете статических характеристик активной нагрузки по напряжению следует иметь в виду, что решающее влияние на вид зависимости оказывает состав потребителей
, (2.49)
где Piнорм - мощность, потребляемая i-м элементом нагрузки при нормальном напряжении;
PΣ - суммарная потребляемая мощность;
Pн(U) и Pi(U) - характеристики суммарной и i-й нагрузок (отн.ед.), причем за единицу принята соответствующая активная нагрузка при нормальном напряжении.
2.1.33. Статические характеристики комплексной нагрузки по напряжению при отсутствии конкретных данных рекомендуется принимать следующими*:
_____________
* Типовые характеристики комплексной нагрузки впервые были предложены в [Л.8]. Здесь приводятся уточненные статистические данные [Л.31]. За единицу приняты нормальные значения напряжения, активной и реактивной мощности. Приведенные выражения справедливы для большего напряжения, чем критическое.
- для активной нагрузки в среднем
Pн ≈ U; (2.50)
с ориентировочным диапазоном вариаций
≈ 0,6 + 0,4U; (2.50, а)
≈ -0,4 + 1,4U; (2.50, б)
- для реактивной нагрузки на стороне 110-220 кВ (в зависимости, от коэффициента мощности нагрузки cosφн при U = 1) в среднем
, (2.51)
с ориентировочным диапазоном вариаций
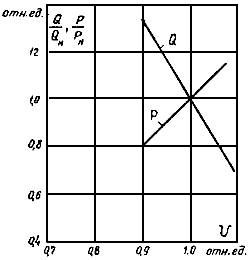
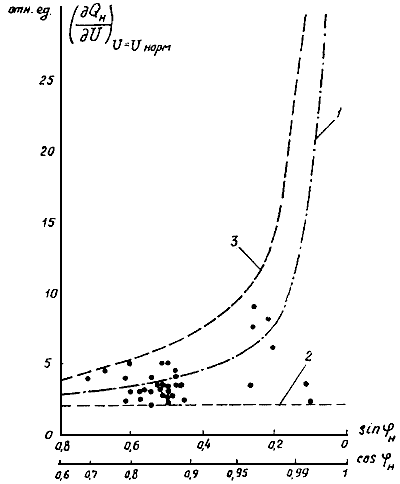
Такое представление реактивной нагрузки соответствует известным в настоящее время данным о ее параметрах и реально имеющей место резко выраженной зависимости значений регулирующего эффекта от значений cosφн (рис. 2.8)*.
_____________
* При увеличении cosφн различие между характеристиками (2.51, а) и (2.51, б), так же, как и между значениями kQ(U), возрастает, однако с ростом cosφн снижается влияние изменений реактивной нагрузки Qн на режим системы. Последнее обстоятельство превалирует, поэтому можно показать, что погрешности расчета режима, обусловленные неточностью задания характеристики Qн = f2(U), для нагрузок с высоким коэффициентом мощности несколько меньше, чем при низких значениях cosφн.
2.1.34. При использовании экспериментальных данных о значениях регулирующих эффектов нагрузки по частоте следует учитывать, что они зависят не только от параметров нагрузки и распределительной сети, но и от условий проведения испытаний. Такая зависимость обусловлена тем, что в процессе понижения частоты, как правило, снижается напряжение (под влиянием нагрузки и АРВ генераторов). Поэтому значения зависят также от значений
:
, (2.52)
где - регулирующий аспект при U = const (для Qн - аналогично).
Значение ориентировочно равно 1,4, если в процессе эксперимента не осуществляется вмешательство в работу АРВ генераторов. Значения
для электроэнергетических систем, по имеющимся данным, составляют 2,0-2,4 (диапазон зарегистрированных вариаций 1,5-2,6). Значения
меняются в очень широких пределах: для нагрузки городов зарегистрированы значения kQ(f) = -(3-15).
Рис. 2.8. Зависимость регулирующих аспектов реактивной нагрузки по напряжению от коэффициента мощности нагрузки:
1 - по формуле (2.51); 2 - по формуле (2.51, а); 3 - по формуле (2.51, б); - значения регулирующего эффекта по данным натурных экспериментов
2.1.35. Динамические характеристики нагрузки следует использовать при выполнении расчетов устойчивости при резких возмущениях (короткие замыкания, АПВ и т.п.) для крупных узлов нагрузки, расположенных вблизи места приложения возмущения и вблизи тех генераторов, устойчивость которых проверяется (см. гл. 6).
2.1.36. Для определения сопротивления токоограничивающего и шунтового реакторов необходимо иметь следующие данные:
- номинальный ток или мощность;
- номинальное напряжение;
- относительное индуктивное сопротивление реактора.
Активное сопротивление реакторов в расчетах обычно не учитывается. Реактивные сопротивления для всех последовательностей одинаковы.
Индуктивное сопротивление токоограничивающего реактора Хр (Ом) определяется по формуле
; (2.53)
то же для шунтового реактора
, (2.54)
где ux - реактивная составляющая падения напряжения в реакторе, в процентах от номинального напряжения реактора;
Uном - номинальное междуфазное напряжение реактора, кВ;
Iном - номинальный ток реактора, кА;
Sном - номинальная мощность реактора, МВ⋅А.
2.1.37. Установки продольной емкостной компенсации (УПК) вводятся в расчетную схему сопротивлением Хс, значение которого обычно выбирается на основе расчетов устойчивости. Иногда значение Хс дается в процентах от реактивного сопротивления соответствующей линии.
2.2. Учет коэффициентов трансформации трансформаторов и автотрансформаторов при составлении расчетных схем. Приведение схемы к базисным условиям
2.2.1. Расчеты режимов и переходных процессов могут выполняться как в именованных, так и в относительных единицах. В последнем случае все параметры схемы и режима выражаются в долях соответствующих величин, принятых за базисные.
2.2.2. При перспективных расчетах на 5, 10, 15 лет вперед допустимо использовать средние номинальные коэффициенты трансформации. При этом среднее расчетное напряжение Uср составляет для каждой ступени трансформации одно из следующих значений: 1150; 750; 500; 330; 230; 154; 115; 37; 20; 15,75; 13,8; 10,5; 6,3; 3,15; 0,525 кВ.
В случае конкретных расчетов, когда известны номинальное коэффициенты трансформации трансформаторов, но отсутствуют данные по установленным ответвлениям трансформаторов, рекомендуется осуществлять приведение параметров схемы по номинальным коэффициентам трансформации трансформаторов.
2.2.3. Если произведение коэффициентов трансформации, входящих в замкнутый контур, отлично от единицы, в расчетную схему должен быть введен дополнительный элемент - идеальный трансформатор. Такой трансформатор характеризуется только коэффициентом трансформации kт при хт = rт = bт = gт = 0.
Идеальный трансформатор включается в замкнутый контур, причем все сопротивления электрической системы приводят к одному напряжению через выбранный расчетный коэффициент трансформации (как правило, за расчетный коэффициент трансформации принимают коэффициент трансформации одного из трансформаторов). Например, если электрические сети 220 и 110 кВ связаны трансформаторами, которые имеют коэффициенты трансформации 242/121 и 209/115, и если считать основным трансформатор с коэффициентом трансформации 242/121, то в точке включения другого трансформатора следует поместить идеальный трансформатор с коэффициентом трансформации 242/121⋅115/209 = 1,1, работающий на повышение напряжения в направлении шин 110 кВ.
2.2.4. При расчетах в системе относительных единиц за базисные величины при определении сопротивлений и параметров режима электрической системы произвольно могут быть выбраны из следующих четырех: кажущаяся мощность, ток, напряжение и полное сопротивление. Обычно в качестве базисных величин удобно принимать мощность Sбаз и напряжение Uбаз на одной из ступеней трансформации. Тогда на этой ступени трансформации базисные сопротивление и ток определяются по формулам
;
. (2.55)
На других ступенях трансформации базисные сопротивление и ток вычисляются по аналогичным формулам с тем лишь различием, что в них подставляется базисное напряжение, предварительно пересчитанное через коэффициенты трансформации к рассматриваемой ступени
;
. (2.56)
Параметры схемы и ее режима (отн.ед.) на каждой из ступеней трансформации определяются по абсолютным значениям с помощью формул
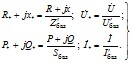
2.2.5. При определении в относительных единицах постоянных времени τ и параметров, характеризующих механическое движение элементов электрической системы, за базисные величины принимаются синхронная частота ωc и время поворота ротора tбаз на угол в один радиан при синхронной частоте вращения, т.е.
. (2.58)
Поэтому в относительных единицах
τс = ωсτ;. (2.59)
Постоянные инерции агрегатов системы должны приводиться к базисной мощности:
. (2.60)
2.3. Преобразование (эквивалентирование) сложных электрических систем
2.3.1. Решение многих практических задач может быть существенно упрощено, если выполнить упрощающие преобразования схемы энергосистемы так, чтобы в расчетной схеме уменьшить количество генераторных станций и узлов нагрузки [Л.32-38].
Преобразованная электрическая система может рассматриваться как эквивалентная исходной системе, но не во всех своих свойствах. С этой особенностью следует считаться при выполнении упрощающих преобразований, осуществляя их при возможно полном сохранении тех свойств системы, которые являются целью исследования.
2.3.2. Оценку возможных упрощений следует делать при составлении схемы замещения электрической системы. При этом надо решить, необходимо ли воспроизводить всю схему системы или достаточно воспроизвести подробно только ее часть, а другую часть упростить. Упрощения могут быть сделаны как весьма грубые, так и более точные. Так, например, при оценке устойчивости протяженной электропередачи, связывающей станцию с мощной энергетической системой, в последней можно произвести грубые упрощения. К числу таких упрощений относится отбрасывание мелких станций и нагрузок, замена небольших станций и нагрузок одной эквивалентной станцией или нагрузкой, перенос нагрузок или станций в точку присоединения другой станции или нагрузки, разрыв слабых связей, объединение общими шинами пунктов, связанных короткими линиями и т.п. В том же случае, когда в задачу входит исследование устойчивости протяженной электропередачи при коротких замыканиях в приемной энергосистеме, часть системы, где предполагают делать короткие замыкания, следует воспроизвести в расчетной схеме с минимальными упрощениями.
2.3.3. Первым этапом упрощения расчетной схемы является исключение второстепенных элементов схемы: мелких нагрузок, параллельных линий, некоторых замкнутых контуров и т.д. При этом осуществляется перенос мелких нагрузок в узловые точки схемы, преобразование пассивных элементов путем осуществления эквивалентных ее преобразований. Следующим этапом расчета может явиться упрощение схем замещения станции, при котором генераторы приводятся к одному эквивалентному.
2.3.4. Значение τj эквивалентного генератора определяется по формуле
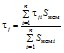
где Sномi - номинальная кажущаяся мощность i-го из объединяемых агрегатов.
Значение постоянной времени эквивалентного генератора* определяется по формуле
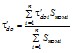
_____________
* Определение терминов см. в приложении 1.
2.3.5. На заключительном этапе выполняются эквивалентные преобразования предварительно упрощенной схемы. При этом рекомендуется применять изложенную ниже методику, предусматривающую замену группы станций одной эквивалентной.
2.3.6. При анализе устойчивости энергосистемы объединение генераторных станций в одну, которую условно можно назвать эквивалентной, должно осуществляться таким образом, чтобы изменения ее угла δ наилучшим образом отразили движение группы объединяемых станций относительно остальных станций системы. Эта задача может быть решена, если в эквивалентную объединяются станции, относительные углы сдвига роторов которых остаются неизменными в течение всего расчетного интервала переходного процесса.
Погрешность эквивалентирования тем меньше, чем ближе реальное движение объединяемых станций к идеально синфазному и, следовательно, находится в прямой связи с тем, насколько удачно выбрана группа станций для объединения. Для такого выбора рекомендуется пользоваться либо опытом эксплуатации, либо результатами ранее выполненных расчетов переходных процессов, либо, наконец, выполнить специальные расчеты режима объединяемых станций в условиях, которые позволят в той или иной мере оценить расхождение относительных углов. В простейшем случае предусматривается объединение станций с близкими значениями постоянных инерции и примерно равными значениями собственных проводимостей и взаимных проводимостей между ветвями объединяемых станций, а также между этими ветвями и ветвью, в которой предполагается расчетное короткое замыкание.
2.3.7. Объединению не подлежат станции, система автоматического регулирования которых может вызвать самораскачивание генераторов в исследуемых режимах системы. Опыт показывает, что самораскачивание в системах практически возможно при применении тех или иных систем сильного регулирования, поэтому станции, снабженные такими регуляторами, должны учитываться в схеме замещения системы как самостоятельные элементы, не входящие и преобразуемые участки схемы.
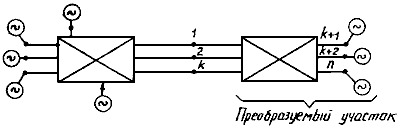
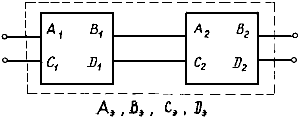
2.3.8. В схеме энергосистемы (рис. 2.9) выделяются узловые точки, к которым подключены генераторные станции системы. Участки сети на рис. 2.9 условно показаны в виде прямоугольников; связь между участками системы осуществляется ветвями 1, 2, ..., k, которые в дальнейшем называются ветвями примыкания преобразуемого участка системы к остальной системе. Для пояснения этого понятия на рис. 2.10 показан участок электрической сети, связывающей преобразуемые и непреобразуемые участки системы, в которой выделена ветвь примыкания.
Рис. 2.9. Условная схема сложной энергосистемы
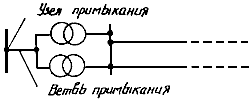
Рис. 2.10. Узел и ветвь примыкания
Преобразуемый участок энергосистемы после эквивалентирования в общем случае будет представлен n-угольником, вершинами которого являются:
- узлы примыкания к неэквивалентируемой части системы (рис. 2.10);
- узел эквивалентного генератора;
- узел нулевого потенциала ("земля").
Большинство применяемых методов требует:
- приведения эквивалентируемого участка к одной ступени напряжения;
- объединения шин генераторов станций преобразуемого участка в один узел эквивалентного генератора.
В случае если узлы примыкания представляются в дальнейших расчетах узлами на разных ступенях напряжения, соответствующие ветви полученного эквивалентного n-угольника становятся трансформаторами.
2.3.9. Для практического использования рекомендуются методы эквивалентирования, основанные на:
1) расчете собственных и взаимных сопротивлений между узлами примыкания, узлом эквивалентного генератора и узлом нулевого потенциала;
2) разнесении нагрузок по правилу моментов в сети, представленной только реактивными сопротивлениями;
3) расчете собственных и взаимных сопротивлений с учетом режима сети и сохранением режима в узлах и ветвях примыкания (см. рис. 2.9).
2.3.10. Основные положения первого метода заключаются в следующем:
а) эквивалентируемый участок системы представляется как активными, так и реактивными сопротивлениями;
б) эквивалентируемый участок системы приводится к одной ступени напряжения;
в) генераторы эквивалентируемого участка объединяются в один эквивалентный генератор на их шинах. Активные и реактивные сопротивления, характеризующие эквивалентный генератор, определяются параллельным сложением соответствующих сопротивлений, объединяемых генераторов. Постоянная инерции определяется по формуле (2.61), а постоянные времени - по формуле (2.62);
г) нагрузки эквивалентируемого участка системы представляются постоянными сопротивлениями, определяемыми по номинальному напряжению сети;
д) эквивалентный n-угольник определяется расчетом собственных и взаимных сопротивлений (проводимостей) по любому из известных методов и программ;
е) баланс мощности для эквивалентного генератора и эквивалентного n-угольника для последующей установки режима определяется ориентировочно вручную.
Этот метод применяется для эквивалентирования удаленных частей энергосистем. К недостаткам метода следует отнести: возможность появления отрицательных активных сопротивлений в эквивалентном n-угольнике, затрудняющих моделирование сети, а также трудности баланса и установки режима в узлах и ветвях примыкания.
2.3.11. Основные положения второго метода по пп. б, в, е совпадают с первым методом, а отличающиеся пп. а, г, д выполняются следующим образом:
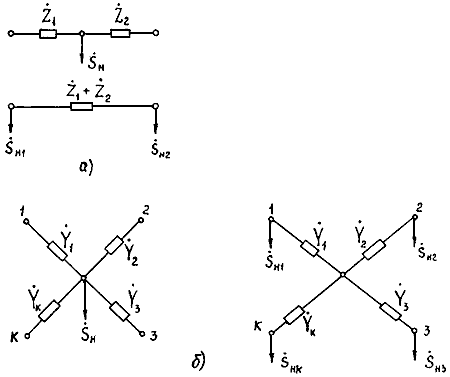
Рис. 2.11. Перенос нагрузок из промежуточной точки:
а - в два соседних узла; б - в несколько соседних узлов
- эквивалентируемый участок системы представляется только реактивными сопротивлениями;
- нагрузки эквивалентируемого участка системы представляются мощностями и разносятся по правилу моментов на шины генераторного напряжения и в узлы примыкания. При этом перенос нагрузки из промежуточной точки в два соседних узла (рис. 2.11) выполняется по формуле
;
. (2.63)
Перенос нагрузки из промежуточной точки в несколько соседних узлов (см. рис. 2.11, б) осуществляется по формуле
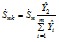
- эквивалентный n-угольник определяется или расчетом собственных и взаимных сопротивлений (проводимостей) по любому из известных методов и программ или с помощью широко известных преобразований "треугольник в звезду", "звезда в треугольник", "многолучевая звезда в многоугольник" и т.д. Поскольку этот метод применяется при ручном эквивалентировании, часто разнесение нагрузок и преобразование сети выполняют последовательно друг за другом - сначала разносят нагрузки, затем преобразуют свободный от нагрузок участок сети, затем снова разносят нагрузки и преобразуют сеть до тех пор, пока все нагрузки не оказываются приложенными в узлах примыкания и в узле эквивалентного генератора, а сеть не превратится в эквивалентны n-угольник. Поскольку при таком методе эквивалентирования при преобразовании сети не учитывается емкостная проводимость линий, следует, подсчитав суммарную генерацию реактивной мощности этими линиями, уменьшить на это значение реактивную мощность нагрузок в окончательной эквивалентной схеме.
Этот метод применяется при эквивалентировании энергосистем, сравнительно удаленных от места возмущения, при эквивалентировании вручную сравнительно небольших участков систем, при представлении электростанций одним эквивалентным генератором и т.д. К недостаткам метода следует отнести трудности расчета режима в эквивалентной схеме.
2.3.12. Третий метод - эквивалентирование с учетом режима сети и сохранением режима в узлах и ветвях примыкания - является наиболее точным и перспективным методом. Связанный с обязательным использованием цифровых вычислительных машин метод позволяет определить режимные параметры эквивалентного генератора и сохранить заранее известный режим в ветвях и узлах примыкания.
Если считать, что станции k + 1, k + 2, ..., n на рис. 2.9, выделенные для объединения, работают синфазно, то условиями эквивалентности режима исходной и преобразованной систем являются [Л.10]: равенство мощностей в ветвях примыкания в обоих схемах; равенство мощности эквивалентной станции сумме мощностей объединяемых станций; определение постоянной инерции эквивалентной станции по (2.61). Предполагается, что синхронные машины замещаются постоянными ЭДС и постоянными сопротивлениями.
2.3.13. При определении параметров схемы замещения преобразованного участка системы следует различать два случая:
- режим преобразуемого участка предварительно рассчитан, причем найдены напряжения во всех узловых точках сети, а также определены ЭДС объединяемых генераторных станций по значению и фазе;
- известна схема электрических соединений преобразуемого участка системы, мощности нагрузок этого участка, мощности, протекающие в ветвях примыкания, и напряжения в соответствующих им узлах (см. рис. 2.10), тогда как для определения режима, работы каждой из объединяемых станций нет достаточно достоверных данных.
Первый случай обычно имеет место при анализе переходных процессов уже существующей системы, для которой хорошо известны и параметры оборудования, и условия экономически целесообразного распределения мощности между ее электрическими станциями. Второй случай имеет место при исследовании перспективных режимов существующих систем или при проектных расчетах. В этих условиях строгий расчет нормального режима может быть затруднен и не всегда оправдан из-за отсутствия полных сведений о ряде параметров системы и ее режима.
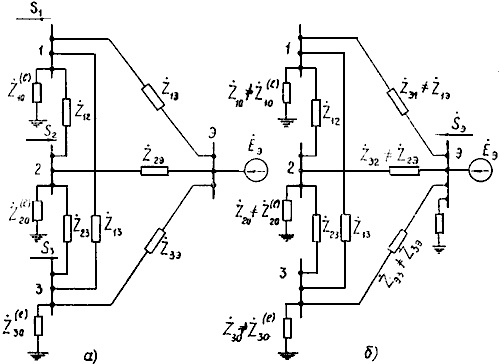
2.3.14. В первом из указанных случаев сформулированные выше условия эквивалентности режима исходной и преобразованной систем удовлетворяются тогда, когда схема замещения преобразованной части системы имеет структуру, показанную на рис. 2.12. Эта схема представляет собой многоугольник с диагоналями и нагрузочными ветвями в узлах примыкания и узле эквивалентной станции. Отличительная особенность схемы заключается в том, что значения входящих в нее сопротивлений должны приниматься различными в зависимости от того, определяется ли режим ветвей примыкания (см. рис. 2.12, а) или эквивалентной генераторной станции (см. рис. 2.12, б).
Рис. 2.12. Схема замещения преобразованной части энергосистемы для частного случая трех ветвей примыкания:
а - для расчета режима ветвей примыкания; б - для расчета режима эквивалентной станции
2.3.15. При определении параметров схемы замещения, предназначенной для нахождения мощностей, токов или напряжений в ветвях и узлах примыкания, а также в непреобразуемой части схемы (см. рис. 2.12, а), ЭДС эквивалентной станции должна выбираться произвольно как по модулю, так и по фазе. Целесообразно эти значения устанавливать такого же порядка, который характерен для ЭДС объединяемых станций. При выбранной ЭДС взаимные проводимости между ветвями примыкания и ветвью эквивалентной станции Ylэ вычисляются по
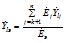
Числитель этой формулы представляет сумму произведений, каждое из которых в качестве сомножителей содержит ЭДС одной из объединяемых станций Ej (j = k, k + 1, …, n) и взаимною проводимость Ylj между ветвью этой j-й станции и той ветвью примыкания l, для которой вычисляется искомая проводимость эквивалентной схемы.
Взаимные проводимости между ветвями примыкания Ylj (i = 1, 2, …, k; l = 1, 2, …, k; l ≠ i) в эквивалентной схеме, также как и собственные проводимости этих ветвей Yll, имеют те же значения, что и в исходной непреобразованной схеме. При известных собственных и взаимных проводимостях проводимости нагрузочных ветвей в схеме замещения определяются выражениями
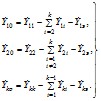
Для частного случая трех ветвей примыкания (см. рис. 2.12)
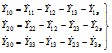
Проводимость нагрузочной ветви эквивалентной станции в рассматриваемой схеме принимается равной нулю.
2.3.16. Параметры схемы замещения, предназначенной для определения мощностей и токов эквивалентной станции (см. рис. 2.12, б), вычисляются в аналогичной последовательности. При принятой ЭДС эквивалентной станции определяются взаимные проводимости между ветвями примыкания и ветвью эквивалентной станции Yэl, но по иной, нежели в первом случае, формуле:
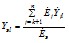
(l = 1, 2, …, k; ).
2.3.17. Взаимные проводимости между ветвями примыкания и собственные проводимости этих ветвей принимаются равными соответствующим значениям в первой схеме, проводимости нагрузочных ветвей вычисляются по формулам
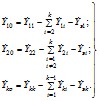
. (2.70)
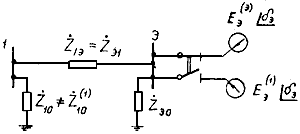
2.3.18. Все приведенные выше формулы справедливы при любом числе ветвей примыкания и объединяемых станций. Для частного случая одной ветви примыкания в схеме возможен также и другой подход к определению параметров схемы замещения преобразуемого участка системы. В этом случае условия эквивалентности режима исходной и преобразованной систем могут быть удовлетворены при одних и тех же сопротивлениях схемы как при определении характеристик режима ветви примыкания и непреобразованной части системы, так и при вычислении мощностей и токов в ветви эквивалентной станции. Однако ЭДС эквивалентной станции при этом должна быть принята разной в зависимости от того, режим какой из ветвей примыкания рассчитывается.
В этом случае при вычислении параметров схемы (рис. 2.13) следует произвольно задаться модулем взаимной проводимости между ветвью примыкания и ветвью эквивалентной станции. Удобно при этом принимать
. (2.71)
Тогда модуль ЭДС эквивалентной станции , которая должна учитываться в схеме при расчете характеристик ветви примыкания, определяется по формуле
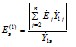
а при расчете режима эквивалентной станции
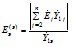
Собственная проводимость в ветви привыкания в преобразованной схеме имеет то же значение, что и в исходной схеме, т.е.
, (2.74)
собственная же проводимость ветви эквивалентной станции определяется выражением
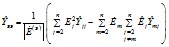
Фазные углы (δэ;Ψэ) комплексных ЭДС эквивалентной станции и взаимной проводимости должны вычисляться по формулам
;
, (2.76)
где γэ1 и γ1э - аргументы комплексных выражений.
;
. (2.77)
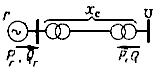
Результаты всех выполненных расчетов позволяют получить все параметры П-образной схемы замещения, показанной на рис. 2.13, причем
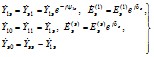
Рис. 2.13. Схема замещения при наличии одной ветви примыкания
Обе ЭДС эквивалентной станции характеризуются одним и тем же фазным углом δэ.
2.3.19. При выполнении преобразований в условиях, когда отсутствуют достоверные данные о режиме работы каждой из объединяемых станций, т.е. при приближенном эквивалентировании, преобразуемый участок системы также представляется схемой замещения, имеющей вид многоугольника с диагоналями и нагрузочными сопротивлениями. Причем в этом случае все параметры схемы, а также ЭДС эквивалентной станции не меняются в зависимости от того, режим какой из ветвей предполагается определять на основании такой схемы.
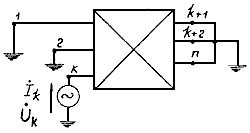
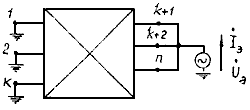
Для их определения составляется полная схема замещения преобразуемого участка системы, в которую нагрузки вводятся постоянными сопротивлениями, вычисляемыми по их заданным мощностям и номинальному напряжению сети. В эту схему входят сопротивления всех элементов системы, ограниченной узлами примыкания и шинами генераторного напряжения объединяемых станций. Применительно к этой схеме вычисляются собственные проводимости ветвей примыкания и взаимные проводимости между этими ветвями (в соответствии с расчетной схемой, приведенной на рис. 2.14). Определяется также собственная проводимость эквивалентной станции, для чего шины генераторного напряжения объединяемых станций считаются соединенными с общим источником напряжения Uэ, а ветви примыкания - замкнутыми накоротко. Расчетная схема для определения собственной проводимости эквивалентной станции показана на рис. 2.15, из которого следует, что
. (2.79)
Рис. 2.14. Расчетная схема преобразуемого участка системы
Рис. 2.15. Расчетная схема для определения собственной проводимости эквивалентной станции
2.3.20. Все эти данные служат для определения напряжения на шинах эквивалентной станции по величине и фазе, взаимных проводимостей между ветвью этой станции и ветвями примыкания, а также нагрузочных сопротивлений эквивалентной схемы замещения. Исходными данными при этом служат также суммарные активная РΣ и реактивная QΣ мощности объединяемых станций, которые устанавливаются приближенно, причем
; (2.80)
Qэ = QΣ = PΣtgφср, (2.81)
где PнΣ - сумма активных мощностей преобразуемого участка системы;
- сумма активных мощностей в ветвях примыкания, которые считаются положительными при направлении к преобразуемому участку;
cosφср - средний коэффициент мощности объединяемых станций, устанавливаемый либо по данным эксплуатации, либо в зависимости от числа трансформаций основного напряжения сети и среднего коэффициента мощности нагрузки.
2.3.21. На основании всех этих величин фазный угол напряжения на шинах эквивалентной станции определяется из следующего трансцендентного уравнения [Л.10], которое может быть решено графоаналитическим методом
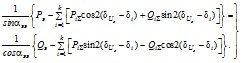
В этой формуле PiΣ и QiΣ - соответственно активная и реактивная мощности, состоящие из нескольких слагающих мощностей, протекающие в i-й ветви примыкания, причем
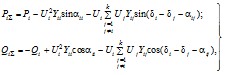
где Pi и Qi - активная и реактивная мощности, заданные в i-й ветви примыкания;
и
- собственные активная и реактивная мощности в i-й ветви привыкания.
Последние члены в формулах (2.83) характеризуют взаимные мощности в ветвях примыкания, определяемые взаимными сопротивлениями и напряжениями в узлах примыкания. В частном случае при равенстве напряжений в узлах примыкания по фазе (δ1 = δ2 … = δk = δi) уравнение приводится к квадратному и, следовательно, решается в общем виде. При этом
, (2.84)
где
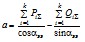
;
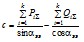
2.3.22. Модуль напряжения на шинах эквивалентной станции определяется по формуле
. (2.85)
Взаимные проводимости между ветвью эквивалентной станции и ветвями примыкания
определяются расчетом из выражения
, (2.86)
причем
. (2.87)
В частном случае при одной ветви примыкания
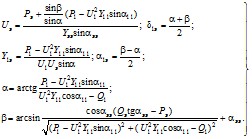
2.3.23. Вне зависимости от принятого метода эквивалентирования правильность его результатов должна быть обязательно проверена. Для этого следует по найденным эквивалентным параметрам преобразованной схемы определить полную мощность ветвей примыкания и полную мощность эквивалентной станции. Совпадение значений этих мощностей с заданными мощностями в ветвях примыкания и с суммой мощностей объединяемых станций свидетельствует об отсутствии ошибок в расчетах эквивалентных параметров.
2.4. Определение собственных и взаимных проводимостей схемы замещения электрической системы
2.4.1. Первый метод заключается в приведении схемы замещения системы путем последовательно выполняемых преобразований к виду многоугольника с диагоналями и нагрузочными сопротивлениями в узлах. При этом применяются в последовательности, зависящей от конфигурации схемы, следующие преобразования: замена треугольника эквивалентной звездой и обратно, замена многолучевой звезды эквивалентным многоугольником, последовательное и параллельное сложение сопротивлений отдельных ветвей.
2.4.2. В многоугольнике, являющемся конечным результатом преобразований, сопротивления сторон и диагоналей представляют собой значения, обратные взаимным проводимостям, с индексами, отвечающими нумерации узлов, между которыми включены указанные сопротивления. Собственные проводимости ветвей схемы Yii определяются по формуле
. (2.89)
Недостатком рассматриваемого метода является отсутствие общего алгоритма расчета, последовательность которого варьируется в зависимости от структуры системы. Этот метод преобразований рекомендуется для определения собственных и взаимных проводимостей только сравнительно простых схем.
2.4.3. Второй метод состоит в том, что все ветви в схеме замещения, для которых определяются собственные и взаимные проводимости, кроме одной (i-й), замкнуты на обратный провод, а в одну из ветвей включен источник напряжения. По результатам этого расчета определяются проводимости
, (i, j = 1, 2, …, n), (2.90)
где n- число ветвей, для которых определяются искомые проводимости.
Расчеты повторяются при включении источника напряжения последовательно во все ветви, для которых определяются собственные и взаимные проводимости.
2.4.4. При использовании ЦВМ для определения проводимостей по данному методу в ветвь каждой из генераторных станций (последовательно) включается источник напряжения, тогда как ЭДС других генераторных станций считаются равными нулю. Результаты такого расчета позволяют определить собственные и взаимные проводимости по формуле (2.90).
2.4.5. Третий метод рекомендуется для схем с двумя генераторными станциями, соединенными схемой электропередачи. Собственные,
и взаимные
сопротивления определяются через комплексные константы
,
,
,
соответствующего четырехполюсника по формулам
;
;
. (2.91)
2.4.6. Для определения констант ,
,
и
анализируемая схема должна быть разбита на участки, для каждого из которых (рассматриваемого в свою очередь в качестве четырехполюсника) известны значения констант. Схема электропередачи с установкой продольной компенсации и шунтирующими реакторами (рис. 2.16) содержит пять последовательно включенных четырехполюсников: два из них соответствуют участкам линии, один - батарее конденсаторов и два - шунтирующим реакторам. Константы четырехполюсников определяются следующим образом:
- для участка линии длиной l,
;
; (2.92)
,
где - волновое сопротивление линии;
- коэффициент распространения волны на единицу длины линии;
Рис. 2.16. Схема замещения электропередачи
- для установки продольной компенсации
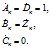
где - сопротивление батареи конденсаторов;
- для шунтирующих реакторов с сопротивлением, равным,
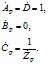
2.4.7. Константы всей совокупности взаимно связанных четырехполюсников вычисляются по правилам сложения четырехполюсников. При последовательном сложении двух четырехполюсников (рис. 2.17) эквивалентные параметры находятся путем перемножения квадратных матриц, составленных из констант первого и второго четырехполюсников:
. (2.95)
Рис. 2.17. Схема сложения двух четырехполюсников
Таким образом,
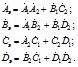
Для n последовательно включенных четырехполюсников эквивалентные константы определяют произведения матриц
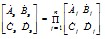
2.4.8. При расчете собственных и взаимных проводимостей очень сложных и разветвленных электрических систем могут встретиться случаи, когда одним расчетом не удается определить все искомые величины из-за ограниченного объема памяти ЦВМ. В этих случаях схему замещения следует разбить на отдельные подсхемы, для каждой из которых вычислить собственно проводимости ветвей примыкания подсхем друг к другу и взаимные проводимости между этими ветвями. В результате такого расчета каждая из выделенных подсхем будет представлена схемой замещения, имеющей вид многоугольника с диагоналями и нагрузочными сопротивлениями в узлах примыкания. Если расчет собственных и взаимных проводимостей выполнен методом преобразований, то в результате непосредственно определяются параметры такой схемы замещения. Если расчет ведется иным образом и результатом его являются значения собственных и взаимных проводимостей для каждой из ветвей примыкания, то для получения значений нагрузочных сопротивлений используется формула
, (2.98)
где q - число сторон и диагоналей многоугольника, связанных с i-м узлом.
Возможно также представление части выделенных из общей схемы участков в виде многоугольника с диагоналями и нагрузочными сопротивлениями при сохранении исходной схемы замещения, составленной из сопротивлений элементов системы для других участков. Такая схема может быть также получена не только при определении собственных и взаимных проводимостей какого-либо выделенного участка системы, но и при упрощающих преобразованиях этого участка с целью уменьшения числа генераторных станций в его расчетной схеме. В каждом из этих случаев полученная схема может служить для вычисления собственных и взаимных проводимостей исходной системы. При выполнении соответствующих расчетов могут быть применены все указанные выше методы.
2.4.9. Если нужно определять собственные и взаимные проводимости для схем, отличающихся друг от друга лишь сопротивлением ограниченного числа элементов, то соответствующие расчеты могут быть существенно упрощены, если за исходные данные принять собственные и взаимные проводимости участка системы, не претерпевающего изменений при переходе от одной расчетной схемы к другой. Тогда изменение схемы может рассматриваться как включение дополнительных сопротивлений в те или иные ее ветви. При включении такого сопротивления в ветвь k схемы, имеющей n ветвей, для которых вычисляются собственные и взаимные проводимости, новые значения искомых проводимостей определяются по формулам
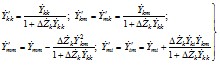
При включении дополнительных сопротивлений в две ветви и более приведенные формулы следует применять последовательно для постепенно усложняющихся схем. Каждая последующая из них должна отличаться от предыдущей включением дополнительного сопротивления лишь в одну из ветвей первоначальной схемы.
2.4.10. Для частного случая двухмашинной схемы замещения системы собственные и взаимные проводимости при включении дополнительных сопротивлений в цепи обеих генераторных станций могут быть найдены по формулам
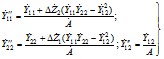
где.
2.4.11. При определении собственных и взаимных проводимостей для ветвей сложной системы при изменениях параметров некоторых элементов и схемы замещения можно также воспользоваться приемом разделения схемы замещения на две части (подсхемы), связанные друг с другом одной ветвью примыкания. Одна из подсхем (I) при этом должна включать ветви, сопротивлениям которых при расчете переходных процессов предполагается придавать несколько значений. Другая подсхема (II) состоит из элементов с неизменяющимися сопротивлениями. При таком подходе подсхема I характеризуется рядом значений собственных и взаимных проводимостей, тогда как каждая из проводимостей ветвей подсхемы II имеет одно единственное значение.
Собственные и взаимные проводимости для схемы замещения всей системы в целом определяются по приведенным ниже формулам, в которые входят собственные и взаимные проводимости, предварительно вычисленные для подсхем I и II. При этом [Л.10] собственная проводимость i-й станции, расположенной в подсхеме I, определяется по формуле
; (2.101)
для взаимной проводимости между ветвью i и ветвью k, расположенной в подсхеме II, справедлива формула
. (2.102)
Взаимная проводимость между ветвями i и n, расположенными в одной и той же подсхеме I, определяется по формуле
, (2.103)
где - собственная проводимость ветви i подсхемы I;
- собственная проводимость ветви примыкания в подсхеме I;
- взаимная проводимость между ветвью i и ветвью примыкания в подсхеме I;
- собственная проводимость ветви примыкания в подсхеме II;
- взаимная проводимость между ветвью k и ветвью примыкания в подсхеме II;
- взаимная проводимость между ветвями i и k в подсхеме I*.
_____________
* По этим алгоритмам в проблемной лаборатории электрических систем МЭИ составлена программа на языке АЛГОЛ-60.
2.4.12. Некоторые частные случаи расчета параметров установившегося режима приведены в приложении 2.
Глава 3. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
3.1. Основные положения
3.1.1. При полном анализе статической устойчивости сложной электрической системы следует рассматривать как общее перемещение роторов, всех генераторов по отношению к синхронно вращающейся оси (т.е. изменения частоты), так и взаимное перемещение роторов генераторов системы при малой взаимной скорости и соответственно взаимную устойчивость их по отношению друг к другу.
3.1.2. В обычных случаях достаточно рассматривать только взаимное перемещение роторов (взаимную или относительную устойчивость) независимо от общего перемещения роторов. При рассмотрении статической устойчивости предполагается только нахождение условий возникновения относительного движения роторов генераторов системы и выявление его характера в начальной стадии движения машин (возможность возникновения монотонно или колебательно нарастающего переходного процесса) без подробного анализа дальнейшего протекания процесса.
3.1.3. При учете динамики автоматического регулирования скорости первичных двигателей анализ статической устойчивости системы может выявить также возможность появления монотонного или колебательного изменений частоты (несмотря на затухание взаимного движения машин) - "неустойчивость частоты". Однако анализ динамики автоматического регулирования скорости первичных двигателей рассматривается как отдельная задача, которая решается для условий автономной работы (одного или двух генераторов, включенных на общие шины станции). Решения, принимаемые на основе такого анализа, практически исключают возможность неустойчивости частоты в системе. При наличии в системе регулирования частоты и активной мощности иногда может возникнуть необходимость в анализе статической устойчивости системы и в отношении возможного изменения частоты (хотя вторичное регулирование частоты и мощности является обычно медленно действующим, что существенно облегчает обеспечение устойчивости регулирования).
3.1.4. Расчеты статической устойчивости электрических систем имеют цель:
а) определение параметров предельных режимов, например предельной передаваемой мощности по тем или иным линиям электропередачи (Рпр) , критического напряжения Uкр основных узловых точек системы, питающих нагрузку, и т.д. [Л.13];
б) определение значений коэффициентов запаса и допустимых потоков активной мощности по линиям электропередачи;
- коэффициента запаса по мощности
, (3.1)
где Р0 - мощность, передаваемая в исходном режиме;
ΔР - нерегулируемый межсистемный переток, он учитывается в случае межсистемной связи;
- допустимой передаваемой мощности по линии при заданном коэффициенте запаса
, (3.2)
где Крн и ΔРн - соответственно значения коэффициента запаса и нерегулируемого межсистемного перетока по мощности, принятые для рассматриваемого режима в соответствии с [Л.1];
- коэффициента запаса по напряжению
, (3.3)
где U0, Uкр - напряжения узловой точки соответственно в исходном и предельном (критическом) режимах;
- коэффициента запаса по настроечным параметрам АРВ
, (3.4)
где Кмакс и Кмин - максимальное и минимальное значения настроечных параметров, соответствующих границе области статической устойчивости;
в) выбор мероприятий для повышения статической устойчивости энергосистем или обеспечения заданной пропускной способности передачи;
г) разработка требований, направленных на улучшение устойчивости и качества переходных процессов. При этом выбирается настройка автоматических регуляторов возбуждения, обеспечивающая требуемую точность поддержания напряжения, и выявляются запасы устойчивости по границе самораскачивания, а также лучшие показатели качества переходных процессов.
Выбор расчетных методов и расчетных средств определяется назначением расчетов, степенью идеализации и сложностью системы.
3.1.5. Так как процесс нарушения статической устойчивости (по характеру изменения относительных углов δ) может быть апериодическим или периодическим, то следует рассматривать две задачи статической устойчивости [Л.10, 12, 39] .
Предполагается, что устройства автоматического регулирования обеспечивают во всех проверяемых режимах отсутствие самораскачивания в электрической системе. В этом случае задача состоит в определении предельного режима электрической системы:
- по условию равенства нулю свободного члена характеристического уравнения, описывающего рассматриваемую систему;
- по соответствующему практическому критерию устойчивости;
- по сходимости специально организованного итерационного процесса расчета режима работы энергосистемы.
Во многих случаях допустимо ограничиваться анализом апериодической устойчивости.
Расчеты статической устойчивости с учетом возможности возникновения самораскачивания проводятся в соответствии с методами, приведенными в [Л.10, 39, 40]. Эти расчеты необходимы в тех случаях, когда в электрической системе появляются новые элементы: мощные удаленные станции с генераторами новых конструкций, с новыми системами возбуждения и регулирования, дальние линии электропередачи и т.п.; когда изменяется конфигурация схемы системы: объединяются две системы, присоединяется промежуточная система, вводятся дополнительные подстанции и т.п.
3.2. Математическое описание сложной электрической системы
3.2.1. При решении задач статической устойчивости сложных электрических систем [Л.10-12] допустим отказ от учета следующих факторов:
- электромагнитных переходных процессов в статорных цепях электрических машин;
- насыщения магнитных цепей синхронных и асинхронных машин.
Насыщение магнитной цепи синхронных машин может быть учтено введением нелинейной характеристики холостого хода и зависимостью реактивных сопротивлений от параметров режима (или использованием постоянных значений этих сопротивлений, но соответствующих режиму насыщения).
3.2.2. Уравнения переходных процессов энергосистемы, содержащей N синхронных машин, соединенных сложными связями, с нагрузками, представленными постоянными сопротивлениями, записываются следующим образом [Л.10, 11].
Уравнения движения роторов синхронных машин (все величины в относительных единицах):
τJip2δI + Pi = Pтi (i = 1, 2, …, N), (3.5)
где Pi, Pтi - электромагнитная мощность и мощность турбины i-й машины.
Выражение электромагнитной мощности i-й синхронной машины имеет вид
, (3.6)
где Ei, Ek - ЭДС синхронных машин.
Формула (3.6) может быть записана через ЭДС или через фиктивные (расчетные) ЭДС EQ [Л.11]; для упрощения записи здесь введено δii = 2αii.
Уравнение электромагнитных переходных процессов в цепи возбуждения i-й синхронной машины [Л.8]:
(i = 1, 2, …, N), (3.7)
где τdoi - постоянная времени обмотки возбуждения,
Eqi, , Eqei - синхронная, переходная и вынужденная ЭДС.
3.2.3. При линеаризации системы уравнений, необходимой для анализа статической устойчивости, в качестве независимых переменных удобно принять углы δk и ЭДС Ek, где k принимают все значения от 1 до N; ЭДС Ek (введена для общности записи) в зависимости от схемы замещения k-й станции может быть равна Eqk для неявнополюсных, EQk для явнополюсных синхронных машин.
Приращение вынужденной ЭДС, зависящее от принятого закона регулирования [Л.10],
, (3.8)
где - передаточная функция регулятора возбуждения, включающая учет переходных процессов в автоматическом регуляторе возбуждения (постоянная времени τp) и в возбудителе (постоянная времени τe) i-й синхронной машины по j-му параметру регулирования Пij.
Суммирование по j-м параметрам Пij необходимо в тех наиболее распространенных случаях, когда регулирование осуществляется по нескольким режимным параметрам (например, по току и напряжению, частоте и напряжению и т.д.).
Передаточная функция АРВ сильного действия по параметру П с учетом постоянных времени дифференцирующих звеньев τ∂ (при некоторой идеализации) определяется по формуле
, (3.9)
где коэффициенты усиления АРВ имеют размерности:
,
,
;
П - режимные параметры в относительных единицах.
3.2.4. Система линеаризованных уравнений имеет следующий вид:
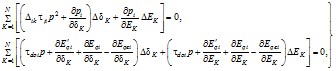
где Δik - символ Кронекера. При i = k Δik = 1. При i ≠ k Δik = 0.
3.2.5. Характеристический определитель для системы (3.10) определяется матричным выражением
, (3.11)
где τJk - диагональная матрица постоянных инерций (размером N×N);
C, B, E, D - квадратные матрицы размером N×N, элементами которых являются следующие выражения:
;
;
;
.
Расчетные выражения частных производных режимных параметров для сложной системы, состоящей из N станций, и для простой системы, содержащей одну автоматически регулируемую станцию, соединенную через сложную связь с приемной системой конечной мощности или с приемной системой бесконечной мощности, приведены в [Л.10].
3.2.6. При анализе влияния АРВ на статическую устойчивость электрической системы ее характеристическое уравнение следует рассматривать в виде
. (3.12)
В первый многочлен входят коэффициенты характеристического уравнения, не зависящие от АРВ рассматриваемой станции. Поэтому он характеризует условия устойчивости системы при отсутствии автоматического регулирования на ней. Второй многочлен отражает влияние на устойчивость регулирования возбуждения выделенной станции. Коэффициенты ΔmП ("единичных добавок") имеют разное выражение для каждого регулируемого параметра Пj и для каждого из m слагаемых второго многочлена. Форма записи (3.12) целесообразна во всех случаях, когда в задачу расчета входит вариация электромагнитных постоянных времени регулятора возбуждения выделенной синхронной машины. Для решения этой задачи рекомендуются методы, описанные в [Л.10].
3.3. Расчеты статической устойчивости в предположении отсутствия самораскачивания
3.3.1. Расчеты статической устойчивости параллельной работы синхронных машин без учета самораскачивания проводятся для получения информации о степени надежности работы энергосистем в основных расчетных режимах. Надежность полученных расчетных данных существенным образом зависит от точности исходной информации. Это положение должно учитываться при выборе методов расчета и степени принимаемой идеализации [Л.41]. Расчеты статической устойчивости при учете возможных отклонений в исходных данных можно проводить по методике, изложенной в [Л.42, 43].
3.3.2. Расчет статической устойчивости при отсутствии самораскачивания выполняется анализом знака свободного члена характеристического уравнения an (при p0): система устойчива, если an > 0. Предельный по апериодической устойчивости режим выявляется путем постепенного утяжеления его параметров, начиная с исходных.
3.3.3. Свободный член характеристического уравнения при регулировании возбуждения синхронных машин системы только по взаимным параметрам выражается в виде определителя (см. приложение 3).
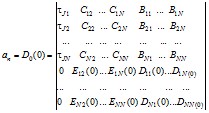
Здесь Eik(0) и Dik(0) соответствуют (3.11) при p = 0.
Элементы этого определителя, а следовательно, и значение an зависят от параметров системы и ее режима, а также от коэффициентов регулирования возбуждения по отклонению параметров Пj.
3.3.4. Режим системы рассчитывается на основе решения следующей системы уравнений [Л.26, 31] при допущении о постоянстве проводимостей
(3.14)
где K0Uk, K0Ik - коэффициенты регулирования по отклонению напряжения и тока;
;
;
;
;
U0k, I0k - уставки регуляторов.
3.3.5. Выбор целесообразных коэффициентов регулирования K0U и K0I при этом монет быть совмещен с расчетами режимных параметров (решением приведенной системы уравнений).
Если среди параметров стабилизации АРВ имеется абсолютный угол, то элементы определителя свободного члена зависят от производных других параметров Пj. Выражение для этого определителя приведено в [Л.10].
Статическую устойчивость системы по знаку свободного члена характеристического уравнения рассчитывают с помощью ЦВМ.
Примеры по определению условий апериодической устойчивости электрических систем даны в приложении 3 и [Л.44].
3.3.6. Расчеты могут быть существенно упрощены допущением о постоянстве ЭДС синхронных машин Ex за сопротивлением x. При этом вносится некоторая погрешность. Значение ЭДС Ex зависит от параметров машины и характеристик регуляторов. Для нерегулируемой машины x = xd = xq, Ex = Eq. При наличии на генераторах АРВ пропорционального действия x = , Ex =
. Если генераторы снабжены АРВ сильного действия, то x = 0 и (т.е. неизменно напряжение на шинах генераторов, а иногда и на шинах высокого напряжения станции). При допущении о постоянстве Ex и x свободный член характеристического уравнения имеет вид [Л.8, 11]:

где α - относительные ускорения роторов станций, взятых попарно, причем нижний индекс указывает, между какими станциями рассматривается перемещение, а верхний - по какому углу берется производная. Например:
;
.
В выражения относительных ускорений входят частные производные мощностей по относительным углам и постоянные инерции синхронных машин. Если в системе одна из станций замещается шинами неизменного напряжения (τI → ∞), то относительные ускорения, а следовательно, и свободный член характеристического уравнения не зависят от соотношения постоянных инерций остальных синхронных машин.
3.3.7. Если принять ряд допущений [Л.8, 45, 46] , то устойчивость сложной системы в отсутствие самораскачивания можно определить по практическим критериям апериодической устойчивости. Выбор практического критерия следует производить, учитывая характер режима, т.е. какие из координат режима являются "сомнительными" с точки зрения устойчивости. Если при закреплении этих координат устойчивость режима можно считать обеспеченной, то, освобождая последовательно эти координаты, можно с помощью соответствующих им критериев определить наличие статической устойчивости системы при полном числе степеней свободы.
3.3.8. Применение критерия dPk/dδki > 0 целесообразно в системах с протяженными или сильно загруженными линиями электропередачи, где при ухудшении исходного режима устойчивость проверяется по углу ЭДС векторов генераторных станций (i и k).
При этом в режиме, соответствующем пределу по мощности системы, имеет место равенство dPk/dδki = 0. Использование этого критерия позволяет свести расчеты апериодической устойчивости системы к определению условий передачи максимальной мощности от станции (или группы станций), что существенно упрощает задачу.
3.3.9. Критерий dΔQгн/dU < 0 следует применять для расчетов устойчивости энергосистем, где имеются узловые подстанции с крупными потребителями. При этом устойчивому режиму в условиях сохранения баланса активной мощности в узле соответствует указанное неравенство, в котором ΔQгн - разность реактивных мощностей, передаваемых от генераторных станций и потребляемых нагрузкой, в узловой точке, U - напряжение узловой точки.
3.3.10. Практический критерий dE/dU > 0 следует применять при проверке устойчивости нагрузки сложной системы, причем под нагрузкой можно понимать и отдельные части энергосистемы. В последнем случае часть энергосистемы, рассматриваемая как нагрузка, представляется в точке примыкания ее к остальной системе не схемой замещения, а зависимостями Рн = f1(U), Qн = f2(U), имеющими место в действительности.
Области применения различных практических критериев статической устойчивости показаны в сводной табл. 3.1. Там же приведены основные расчетные выражения. Примеры расчетов статической устойчивости по практическим критериям приведены в [Л.44]. Способ оценки погрешностей в значениях предела по статической апериодической устойчивости см. в приложении 4.
3.4. Утяжеление исходного режима энергосистемы
3.4.1. Выбор способа утяжеления режима ("траектории утяжеления") в условиях реальных энергосистем не является однозначным.
3.4.2. Практически принимаемый способ утяжеления режима должен учитывать свойства рассматриваемой системы и те критерии устойчивости, по которым определяется предельный режим. Рекомендуются следующие способы утяжеления режима или комбинации их:
- перераспределение активных мощностей между генераторными станциями;
- увеличение нагрузки на наиболее загруженных узловых подстанциях;
- снижение напряжения в тех или иных узлах системы.
3.4.3. Утяжеление режима путем перераспределения активных мощностей между генераторными станциями следует применять для систем, содержащих протяженные или сильно загруженные линии электропередачи. Этот способ утяжеления позволяет определить пропускную способность рассматриваемых линий. Для оценки апериодической устойчивости используется критерий dP/dδ > 0.
При данном способе утяжеления режима для каждой конкретной системы должны быть выбраны передающая и балансирующая станции (или группы их) с таким расчетом, чтобы увеличивающийся поток активной мощности проходил по линиям электропередачи исследуемого направления или через определенное сечение.
В ряде случаев последнее сразу установить трудно, поэтому рассматриваются различные варианты перераспределения активных мощностей, что позволяет выявить потенциальные возможности системы, различного рода ограничения, имеющийся на генераторных станциях резерв по активной мощности и другие особенности схемы.
3.4.4. Правильность выбора общей мощности и числа станций, между которыми в процессе утяжеления режима ведется перераспределение активных мощностей, следует контролировать вариантными расчетами, поскольку увеличение числа станций, мощность которых во всех утяжеленных режимах фиксирована, снижает расчетную величину пропускной способности электропередачи.
При выборе станций, между которыми производится перераспределение мощностей, следует учитывать, насколько данная траектория утяжеления режима вероятна в условиях рассматриваемой энергосистемы. Суждение, хотя бы приближенное, о вероятности реализации на практике того или иного варианта утяжеления режима нужно для правильной оценки получаемых в расчетах значений коэффициентов запаса по устойчивости.
3.4.5. При утяжелении режимов концентрированных систем, т.е. таких, где генераторные станции и узлы с мощной нагрузкой расположены вблизи друг от друга, рассматривается увеличение нагрузки основных узлов приемной части системы или снижение напряжения в узловых точках (т.е. снижение некоторых ЭДС). Эти же способы утяжеления режима системы следует применять при исследованиях статической устойчивости узлов нагрузки. Предельный режим в обоих случаях определяется по знаку свободного члена характеристического уравнения или по практическим критериям
dΔQгн/dU < 0, dE/dU > 0.
3.4.6. В проектных расчетах последовательно утяжеляемых режимов допускается перегрузка части оборудования, но если при подходе к пределу устойчивости перегрузки оказывается во много раз больше допустимых, то это свидетельствует о том, что выбранный способ утяжеления режима является нереальным.
Вопрос о необходимости учета ограничений следует решать в зависимости от того, является ли расчет проектным, исследовательским или эксплуатационным. Такое ограничение, как потолок возбуждения генераторов, следует учитывать всегда. Неучет ряда ограничений оправдывается тем, что при проведении проектных разработок иногда неизвестны размещение резервов в системе, точное значение нагрузок и возможность появления новых потребителей.
3.4.7. В расчетах, выполняемых для нужд эксплуатации энергосистем, в начале следует провести серию расчетов режимов с проверкой устойчивости при длительно допустимых эксплуатационных ограничениях*. Если достигается предел устойчивости системы, то расчет заканчивается. Если предел устойчивости не достигнут, а нарушается какое-либо из ограничений, то может быть произведена вариация режима внутри заданных эксплуатационных ограничений. Наконец, если эта возможность исчерпана, то эксплуатационные ограничения могут быть сняты и заменены кратковременно допустимыми техническими ограничениями**.
_____________
* К эксплуатационным ограничениям относятся ограничения, обусловленные тепловым режимом машин и элементов сети, уровнем напряжения в заданных точках системы, желаемыми перетоками в некоторых линиях связи, располагаемой реактивной мощностью синхронных машин и т.д. Действие автоматических устройств учитывается при этом (в расчете утяжеления режимов) по внешним характеристикам (статические характеристики нагрузки должны учитывать, хотя бы ориентировочно, влияние автоматического регулирования напряжений в сетях).
** К техническим ограничениям относятся: кратковременно возможная перегрузка машин и трансформаторов, кратковременно допустимое изменение значений напряжения и т.д. Кратковременность рассматриваемых режимов зависит также от уставок времени срабатывания соответствующих релейных защит. Действие автоматических устройств учитывается при этом (в расчете утяжеления режимов) по "внутренним" характеристикам с учетом быстродействия (статические характеристики нагрузки не должны учитывать медленнодействующие системы регулирования напряжения в сетях и мощности или тока у потребителей).
Таким образом, получается достаточно полная и реальная оценка запаса устойчивости с дифференциацией в отношении длительно допустимых режимов или режимов, кратковременно возможных по условиям статической устойчивости, но требующих немедленного вмешательства (автоматического или оперативного) для дальнейшего перехода к длительно допустимому режиму. Запас устойчивости определяется в отношении заданных режимных параметров (допустимого изменения нагрузки, или перетока в линиях, или напряжений в узлах системы).
3.4.8. В этих расчетах нагрузка может представляться:
- постоянным полным сопротивлением, найденным по параметрам исходного режима;
- неизменными активными и реактивными мощностями;
- статическими характеристиками по напряжению.
При рассмотрении устойчивости нагрузок последние должны быть заданы статическими характеристиками по напряжению. Аналогичное требование имеет место при выявлении предельного режима системы по практическому критерию dΔQгн/dU < 0. Учет статических характеристик нагрузки по напряжению требуется тогда, когда в процессе утяжеления режима существенно изменяется напряжение в нагрузочных узлах, в частности, исследование статической устойчивости послеаварийного режима предполагает учет действительных характеристик нагрузок.
Примеры определения пределов по мощности при разных способах представления нагрузок даны в [Л.44].
Таблица 3.1
Типичная схема (Ег = const) | Простейшая электрическая система (генератор шины) | Два эквивалентных генератора соизмеримой мощности работают на общую нагрузку | Многомашинная система, имеющая узловую точку | Эквивалентный генератор, питающий через ВЛ нагрузку соизмеримой мощности | |
Способ задания нагрузки | Zн = const | Статические характеристики по напряжению Рн = f1(U), Qн = f2(U) | Статические характеристики по напряжению Рн = f1(U), Qн = f2(U) | Эквивалентный асинхронный двигатель (см. гл. 6) | |
Схема замещения системы | |||||
Критерий статической устойчивости | |||||
Условие подхода к пределу при получении критерия | Рг = var | U = var | Pн + jQн = var или EI = var | U = var; Pн + jQн = var | P = var |
Независимая переменная | δ | δ12 | Uк | U | S |
Определяемый параметр режима | Рпр, Кр | Рпр, Кр | Uк.кр, КU | Uкр, Екр, КU , КЕ | Рпр, Sкр, Uкр, Кр, КU |
Расчетные выражения |
|
|
|
|
|
Графическое представление критерия устойчивости | |||||
3.5. Статическая устойчивость энергосистемы с учетом самораскачивания
3.5.1. Расчеты статической устойчивости энергосистемы с учетом самораскачивания проводятся, когда имеется опасность его возникновения.
В электрической системе, находящейся в эксплуатации, такая опасность может возникнуть при резком изменении конфигурации схемы (объединении двух систем, включении промежуточных систем, присоединении новой ВЛ и т.п.) вблизи станций, у которых проявляется тенденция к самораскачиванию. Эти станции характеризуются либо большой удаленностью, малыми запасами устойчивости и работой при углах δ, близких к 90°, либо ухудшенными параметрами синхронных машин (малыми постоянными инерции, большими реактивными сопротивлениями), либо трудностями настройки автоматических регуляторов возбуждения, особенно АРВ сильного действия. Такие станции должны быть выявлены на первом этапе расчета статической устойчивости. В этом случае задача исследования - выявить причину и устранить возможность самораскачивания с помощью корректировки рабочей настройки АРВ или введения каких-либо дополнительных мероприятий.
3.5.2. На стадии проектирования составляются технические требования к системе возбуждения и автоматическому регулированию возбуждения синхронных машин по условию обеспечения статической устойчивости. Под этим понимается либо выбор схемы возбуждения (если рассматривается несколько вариантов ее исполнения), либо способа регулирования возбуждения (закона регулирования, структурной схемы и параметров регулирования), либо схемы присоединения измерительных элементов АРВ, либо его конструктивных параметров.
При выборе способа регулирования возбуждения предпочтение следует оказывать тому варианту, при котором при равных пределах статической устойчивости:
- обеспечивается наиболее простая и надежная схема присоединения измерительного элемента;
- предъявляются наименее жесткие требования к конструктивным параметрам: не требуется специального уменьшения постоянной времени возбудителя, выпрямительных и дифференцирующих звеньев автоматического регулятора возбуждения;
- обеспечивается возможность постоянной настройки АРВ при всех возможных режимах и схемах проектируемой электрической системы (схема нормального и послеаварийного режима, выдача мощности станцией в одном или двух направлениях, схема с включенными или отключенными устройствами продольной и поперечной компенсации, реверсивный режим работы электропередачи, схема с включенными или отмеченными промежуточными энергосистемами или углами нагрузок и т.д.);
- обеспечиваются наибольшие области устойчивости относительно настроечных значений коэффициентов регулирования;
- обеспечиваются лучшие показатели качества переходных процессов.
3.5.3. Настроечные параметры, входящие в закон регулирования возбуждения, при решении задачи выбора области рабочих настроек АРВ разбиваются на две группы:
1) коэффициенты регулирования по отклонениям режимных параметров К0П.
2) коэффициент регулирования по производным режимным параметрам К1П; К2П.
3.5.4. Коэффициенты регулирования К0П выбираются:
- по условию поддержания напряжения в заданной точке энергосистемы с требуемой точностью;
- по условию обеспечения заданного предела апериодической устойчивости (т.е. полной или частичной компенсации реактивного сопротивления генератора или трансформатора или его и другого).
Оба эти условия, как правило, выполняются при регулировании по отклонению напряжения с коэффициентом усиления К0U =50÷100 ед.возб.х.х./ед.напр. (или 25÷50 ед.возб.ном /ед.напр.)* и отклонению тока, либо в виде компаундирования измерительного элемента напряжения АРВ, либо в виде регулирования по отклонению тока.
_____________
* Размерность значений коэффициентов ед.возб.х.х/ед.напр. применяется в теоретических и практических расчетах, размерность ед.возб.ном/ед.напр. - при маркировке АРВ.
3.5.5. Коэффициенты регулирования по производным режимных параметров (стабилизирующие) выбираются из условия исключения самораскачивания в системе во всех возможных режимах при заданных коэффициентах по отклонению.
Стабилизирующие параметры АРВ сильного действия условно подразделяются на основные и дополнительные. Основные играют главную роль в обеспечении условий отсутствия самораскачивания в системе (например, регулирование по отклонению частоты и ее первой производной - К0f*, К1f), в то время как дополнительные (например, К1U) предназначены для устранения самораскачивания в режимах холостого хода генератора, либо для улучшения условий выбора основных стабилизирующих параметров в рабочих режимах (увеличения размеров области устойчивости в плоскости основных параметров), либо для улучшения показателей качества.
_____________
* Регулирование по отклонению частоты дает эффект, близкий к регулированию по первой производной абсолютного угла, но имеет некоторые дополнительные недостатки.
3.5.6. Исследования статической устойчивости с учетом самораскачивания [Л.47-52] целесообразно проводить путем построения областей устойчивости в координатах основных стабилизирующих параметров АРВ выделенной станции для нескольких, наиболее характерных режимов работы электрической системы (выявленных при анализе апериодической устойчивости). Если в результате расчетов оказывается, что размер общего участка построенных областей недостаточен [Л.10], то при существующих АРВ с постоянной настройкой это может быть причиной ограничения предельно передаваемой мощности.
3.5.7. Изменение коэффициентов регулирования в современных АРВ производится переключателями, шкала которых, как правило, имеет десять делений. Практически необходимо, чтобы устойчивость системы обеспечивалась не при одном делении шкалы коэффициентов, соответствующим выбранной настройке, а по меньшей мере при трех соседних делениях. При этой минимально необходимый размер области устойчивости (по каждому коэффициенту регулирования), удовлетворяющий этому требованию в единицах деления шкалы, должен равняться Кнастр ± 0,1Кмакс. Режим, при котором практически исключается возможность работы при постоянных коэффициентах регулирования, является предельным и определяет Рмакс, δмакс или Uкр. Чтобы уточнить существование такого ограничения, следует повторить расчеты с учетом некоторых уточняющих факторов (например, учет насыщения синхронной машины, электромагнитных переходных процессов в демпферных контурах ротора, реальных характеристик нагрузок энергосистемы и др.).
3.5.8. Для устранения ограничения предельно передаваемой мощности следует рассмотреть мероприятия по улучшению закона регулирования, т.е. по изменению или расширению множества настроечных параметров, внутри которого можно выбирать рабочую настройку АРВ.
В качестве таких мероприятий следует рассмотреть целесообразность пересоединения измерительного элемента АРВ к измерительным трансформаторам (тока или напряжения), включенный в других точках станции (выводы генератора, шины станции и т.д.), введения дополнительных стабилизирующих устройств в систему регулирования, целесообразность использования (в кратковременных режимах) рабочей настройки АРВ, лежащей вне области (за безопасной границей) статической устойчивости, изменения структурной схемы (иногда путем введения дополнительных обратных связей) или конструктивных параметров системы возбуждения и регулирования.
Для выбора структуры АРВ, при которой устраняются ограничения предельно передаваемой мощности, целесообразно применять разработанные в МЭИ методы синтеза [Л.53-55].
3.5.9. При расчетах статической устойчивости с учетом самораскачивания могут применяться критерий Гурвица, либо критерий Рауса, либо метод D-разбиения в соединении с критерием Михайлова. Последний наиболее эффективен для сравнительно сложных систем и при решении задач, связанных с выбором систем возбуждения и регулирования.
Описания критериев устойчивости приведены в [Л.12, 39], в приложении 5 дается ряд примеров решения задач для простых схем.
3.5.10. Построение областей устойчивости в сложной энергосистеме (многомерных областей устойчивости) может быть выполнено следующим упрощенным способом.
Вначале АРВ задаются некоторыми значениями настроечных параметров для всех машин, кроме выделенной, для которой рассчитывается область устойчивости и выбираются настроечные параметры внутри нее. Затем для второй синхронной машины с АРВ рассчитывается область устойчивости с учетом выбранных параметров АРВ на каждой машине и заданных на остальных. Расчеты продолжаются до тех пор, пока не будут определены области устойчивости в плоскости настроечных параметров АРВ каждой синхронной машины. В качестве первой синхронной машины, для которой рассчитывается область устойчивости, следует брать машину с наиболее тяжелым режимом (например, наиболее удаленную и загруженную), поскольку задаться настроечными параметрами АРВ такой машины значительно труднее, чем на остальных (ввиду уменьшения размеров области устойчивости с увеличением загруженности и удаленности машины). Таким образом, по рассмотренному способу вначале выбирается точка, достаточно удаленная от границы области устойчивости, лишь в плоскости двух параметров (путем расчета области устойчивости в плоскости настроечных параметров АРВ выделенной синхронной машины при заданных настоечных параметрах АРВ остальных машин) и далее проводятся сечения многомерной области устойчивости плоскостями, проходящими через эту точку (путем расчета областей устойчивости в плоскости настроечных параметров АРВ остальных синхронных машин). Этим достигается значительное сокращение объема вычислений по сравнению с другими методами.
3.5.11. Для предварительного задания коэффициентов основных стабилизирующих параметров АРВ сильного действия следует рассмотреть условия устойчивости основного и относительного движения, характерные для схем электрических систем, обладающих внутригрупповой симметрией.
Область устойчивости относительного движения между параллельно работающими синхронными машинами обычно ограничивает максимально допустимые коэффициенты регулирования по производным, а область устойчивости основного движения в режимах больших нагрузок - минимально допустимые.
3.5.12. Расчет областей устойчивости относительного движения проводится для схем эквивалентный генератор - шины неизменного напряжения в точке объединения генераторов. В качестве предварительно задаваемых коэффициентов основных стабилизирующих параметров АРВ следует выбирать коэффициенты, расположенные внутри области относительного движения, рассчитанной для номинальной нагрузки синхронной машины.
3.5.13. При невозможности строгого разделения движения на основное и относительное (например, при использовании для стабилизации АРВ только общих для всех синхронных машин станции параметров) с некоторым приближением, вполне оправданным для целей предварительного задания коэффициентов стабилизации, можно строить область относительного движения по схеме станция - шины неизменного напряжения, где в качестве таких шин выбирается ближайшая к данной станции узловая точка системы.
3.5.14. Порядок проведения расчетов статической устойчивости сложной системы, содержащей несколько станций (подстанций) с АРВ сильного действия:
а) выбираются коэффициенты регулирования по отклонению режимных параметров всех АРВ (исходя из заданной точности поддержания напряжения на шинах станции) и коэффициенты дополнительных стабилизирующих параметров (по условию устойчивости генераторов на холостом ходу);
б) рассчитываются области устойчивости относительного движения в плоскости коэффициентов основных стабилизирующих параметров каждой эквивалентной синхронной машины в режиме номинальной мощности и выбираются (на всех станциях, кроме выделенной) наибольшие коэффициенты внутри области;
в) рассчитываются области устойчивости основного движения в плоскости основных стабилизирующих параметров АРВ выделенной эквивалентной синхронной машины для заданных характерных режимов;
г) если область устойчивости для выделенной станции не существует, то вводятся дополнительные стабилизирующие параметры для АРВ этой станции и расчет (п. 3) повторяется;
д) если область устойчивости для выделенной станции существует, то выбираются коэффициенты внутри нее (равноудаленные от границ) и далее проводится расчет областей устойчивости основного движения последовательно для всех остальных синхронных машин системы.
Некоторые вопросы построения областей устойчивости для АРВ сильного действия с применением D -разбиения рассмотрены в приложении 6.
Глава 4. ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ ЭНЕРГОСИСТЕМ
4.1. Допущения и предпосылки
4.1.1. Для анализа динамической устойчивости расчетная схема описывается системой дифференциальных уравнений, которые в общем случае решаются численным интегрированием с помощью ЦВМ.
Для электрических малин используются либо полные уравнения Парка-Горева (2.31), либо те же уравнения, но без учета переходных, процессов в статоре [те жe уравнения, но с заменой (2.31, а) и (2.31, б) на (2.32, а), (2.32, б)], либо уравнения без учета демпферных контуров (2.33). Последние известны в различных формах записи.
4.1.2. Уравнения Парка-Горева (в большинстве случаев упрощенные) следует применять:
- для расчетов устойчивости отдельной группы генераторов или одного генератора с детальным учетом влияния многих факторов;
- в сложной энергосистеме для учета генераторов наиболее мощных электростанций, чьи переходные процессы, особенности регулирования и т.п. могут оказать решающее влияние на результата расчетов;
- для генераторов, ближайших к месту приложения возмущения.
Для остальных генераторов следует рассмотреть возможность их упрощенного описания - без учета демпферных контуров или = const.
4.1.3. Во многих практических случаях при анализе динамической устойчивости учет апериодических составляющих токов статора не является обязательным. Это обусловливается тем, что в электромеханическом переходном процессе основное значение имеет переходная составляющая токов статора.
4.1.4. Модели синхронных машин, описываемые теми или другими уравнениями, должны дополняться уравнениями учета динамики автоматического регулирования возбуждения (АРВ) и скорости первичных двигателей (АРС), а также учета динамических характеристик нагрузок в углах электрической сети.
4.1.5. При выборе упрощений математического описания энергосистемы решающую роль играют конкретные цели расчетов и особенности рассматриваемой энергосистемы. То же самое относится и к упрощениям при учете величин, вида и места приложения расчетных возмущений.
4.1.6. Упрощенное моделирование генераторов (постоянной ЭДС за сопротивлением
) обычно оправдано для генераторов, удаленных от места приложения КЗ настолько, что изменение напряжения на их шинах не превышает 15-20% при пропорциональном регулировании возбуждения. В случае быстродействующих систем возбуждения часто требуется более точное моделирование синхронной машины.
4.1.7. Упрощенное моделирование часто допустимо для генераторов, работающих в концентрированных энергосистемах, соединенных слабыми связями, при рассмотрении возмущений на межсистемных электропередачах.
4.1.8. Нагрузку при удаленных КЗ и небольших (до 15%) изменениях напряжения допустимо учитывать неизменным полным сопротивлением, вычисленным по параметрам исходного доаварийного режима. Такое представление возможно и для более точных расчетов, если изменения напряжения на нагрузках в электромеханическом переходном процессе не превысят 10%. В противном случае следует представлять нагрузку ее динамическими характеристиками, например, уравнениями эквивалентного асинхронного двигателя и статической нагрузкой (см. гл. 6) или переменным полный сопротивлением, определяемым по заранее построенным типовым кривым [Л.4, 8, 56].
Количество элементов в расчетной схеме, соответствующей исследуемой электрической сети, является существенным фактором, ограничивающим применение тех или иных расчетных средств и приемов, моделей синхронных машин и их систем регулирования. Способы и методы упрощения расчетных схем замещения описаны в гл. 2.
4.2. Исследования динамической устойчивости в одном-двух циклах изменения относительных углов синхронных машин
4.2.1. Подобные исследования динамической устойчивости обычно выполняются на первых этапах перспективного проектирования энергосистем, а также при разработке перспективных режимов в эксплуатации, т.е. в случаях ориентировочных расчетов, когда требования к точности получаемых результатов сравнительно невелики. При этом допускается значительное упрощение расчетных схем замещения, расчетных условий, моделей синхронных машин с системами регулирования и нагрузок. Чаще всего эти исследования выполняются при постоянстве ЭДС генераторов за некоторым реактивным сопротивлением (обычно ) и представлении нагрузок неизменными полными сопротивлениями с возможные введением ряда уточнений.
4.2.2. Простейшая система. Если анализ динамической устойчивости можно свести к исследованию простейшей схемы замещения, содержащей эквивалентный генератор и шины неизменного напряжения (и частоты) или два генератора конечной мощности, то решение задачи можно существенно упростить. Соответствующая математическая модель ограничивается уравнением движения эквивалентного генератора, которое особенно упрощается при неучете активных сопротивлений (и, следовательно, неучете асинхронного момента). В общем случае оно имеет следующий вид
. (4.1)
4.2.3. Сметена, содержащая два эквивалентных генератора, описанных упрощенными уравнениями, сводится (при исследовании только их относительного движения) к схеме генератор - шины неизменного напряжения следующий образом.
Дифференциальные уравнения относительного движения роторов двух синхронных машин конечной мощности
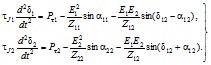
можно привести к простейшей форме уравнения движения эквивалентного генератора, работающего на шины неизменного напряжения
, (4.3)
если принять, что
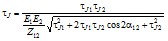
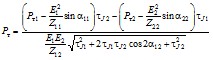
.
4.2.4. Ориентировочные расчеты, выполняемые для простейших схем, обычно имеют целью:
- проверить выбранные уставки релейной защиты для заданного режима;
- наши предельное время отключения повреждения или АПВ;
- найти предельную мощность станции по условиям динамической устойчивости.
Здесь возможно применение разнообразных расчетных приемов, в том числе основанных на ручном счете с помощью логарифмической линейки, клавишных вычислительных машин, таблиц, номограмм и т.п. Указанные приемы иллюстрируются в приложении 7 на примере конкретных расчетов по уравнению (4.1).
4.2.5. Метод последовательных интервалов. Общий способ решения уравнения типа (4.1) или более сложных систем подобных уравнений заключается в их численном интегрировании. Применительно к исследованию динамической устойчивости электрической системы традиционным методом является метод последовательных интервалов. Методика расчета методом последовательных интервалов подробно освещена в [Л.4, 8, 11]. При рассмотренных выше допущениях величина расчетного интервала при расчетах вручную или на статических моделях энергосистем берется в пределах 0,05-0,1 с. Меньшее значение следует принимать для синхронных машин с малыми постоянными инерции τJ. В программах расчета синхронной динамической устойчивости на ЦВМ, реализующих метод последовательных интервалов, можно брать Δt = 0,02 с, если не применяются полные уравнения Парка-Горева.
4.2.6. В исследованиях динамической устойчивости в 1-2 циклах изменения относительных углов синхронных машин применительно к современным автоматически регулируемым энергосистемам, содержащим протяженные линии электропередачи сверхвысокого напряжения с УПК, крупные генераторы, нередко требуется уточнение моделей генераторов и нагрузок по сравнению с упрощенным представлением неизменными ЭДС и полными сопротивлениями.
Для генераторов это прежде всего учет АРВ, а также синхронной и переходной явнополюсностей xd ≠ xq ≠ . Такому представлению соответствуют уравнения (2.33). Их целесообразно использовать в записи через ЭДС
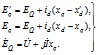
где - вектор напряжения на шинах генератора;
- вектор тока;
id - составляющая по оси d;
- проекция переходной ЭДС
на ось q;
- вектор фиктивной ЭДС за сопротивлением xq.
Вектор совпадает с направлением поперечной оси q (его фаза точно соответствует угловому положению ротора).
Изменение потокосцепления ротора по продольной оси, обусловленное реакцией статора и действием АРВ
, (4.5)
где Eqe - ЭДС, пропорциональная напряжению обмотки возбуждения.
Активная мощность генератора
P = Udid + Uqiq. (4.6)
Уравнение движения не зависит от допущений, сделанных при учете электромагнитных процессов
ωcτjps + P = Mт*. (4.7)
_____________
* Принимается, что изменения скорости малы, при этом момент турбины равен ее мощности.
Уравнения (4.4)-(4.7) образует систему уравнений, известную как уравнения Лебедева-Жданова или уравнения Лонглея.
Уравнение (4.5) дополняется моделью АРВ, который в простейшем случае описывается уравнением апериодического звена 1-го порядка с эквивалентной постоянной времени регулятора возбуждения и возбудителя. В качестве параметра регулирования используется отклонение значения напряжения на шинах генератора. Также предусматривается простейший учет ограничения напряжения возбуждения сверху и снизу. Описанная упрощенная модель АРВ соответствующим образом модифицируется в зависимости от конкретных особенностей системы АРВ (электромагнитная, быстродействующая релейная форсировка и релейное развозбуждение и т.д.). Действие системы регулирования первичного двигателя приближенно учитывается принятием Mт = const, либо заданием в графической или табличной форме закона регулирования Mт = f(t) при учете системы быстродействующего управления моментом первичного двигателя.
4.2.7. Уточнение модели нагрузки может быть достигнуто различными способами (см. гл. 6). В рассматриваемых уравнениях целесообразно учитывать зависимость эквивалентного полного сопротивления комплексной нагрузки от изменения напряжения нагрузочного узла в переходном процессе. Это может быть сделано, например, вычислением на каждом расчетном интервале результирующего полного сопротивления схемы замещения эквивалентного асинхронного электродвигателя по текущим значениям его скольжения и напряжения нагрузочного узла, используя уравнение движения двигателя. При этом параметры схемы замещения, электрические и механические характеристики двигателя приближенно описывают усредненные динамические характеристики угла нагрузки.
4.3. Исследование динамической устойчивости при уточненном моделировании синхронных машин и нагрузок
4.3.1. Уточнение моделей синхронных машин и нагрузок при исследованиях динамической устойчивости возможно по двум направлениям:
1) использование более полного математического описания переходных процессов в элементах электрической системы на основе точных уравнений Парка-Горева;
2) уточнение моделей, описываемых упрощенными уравнениями, введением дополнительных слагаемых, коэффициентов, полуэмпирических зависимостей и т.п.
Рамки первого направления ограничиваются не только трудностями вычислительного порядка, но главным образом неточным знанием необходимых параметров элементов электрической системы, что может привести к большей погрешности результатов по сравнению с погрешностями, обусловленными упрощением моделей. Использование уравнений Парка-Горева для моделирования синхронных машин требует уточнения модели их систем AРB и АРС. Детальное моделирование всех элементов этих устройств, включая дифференциальные уравнения, связывающие передаточные функции отдельных частей регулятора, а также инерционность и насыщение магниевых цепей, практически осуществимо главным образом для простых схем и в специальных случаях.
4.3.2. Для практических целей часто используют уравнения Лебедева-Жданова, уточняя модели AРB и АРС [Л.57, 58]. Применяют представление системы регулирования с упрощенным разделением элементов регулятора и выделением каналов по отклонениям и производным тех или иных режимных параметров. В большинстве случаев допустимо использовать модель АРВ, отображающую как обычное пропорциональное, так и сильное регулирование по отклонению и первым производным тока, напряжения и частоты с релейной форсировкой возбуждения при снижении напряжения на шинах генератора до заданной уставки Uф:
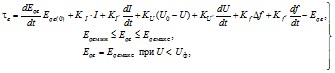
где τe - эквивалентная постоянная системы АРВ;
Eqe(0) - независимая составляющая напряжения возбуждения;
KI, , KU,
, Kf,
- коэффициенты регулирование по току, напряжению, отклонению частоты и их производным;
U0 - уставка АРВ по напряжению статора;
Uф - уставка АРВ по релейной форсировке возбуждения.
При необходимости эта модель может дополняться с учетом постоянных времени по отдельным каналам регулирования и регулятора в целом.
4.3.3. Модель системы регулирования скорости первичного двигателя учитывается апериодическим звеном 1-го порядка с введением ограничений
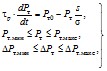
где τp - постоянная времени регулятора;
Pт0 - уставка регулятора по мощности;
s - скольжение генератора относительно синхронной оси;
σ - коэффициент статизма регулятора;
ΔPт - приращение мощности первичного двигателя за шаг интегрирования;
ΔPт.мин, ΔPт.макс - приращения мощности первичного двигателя за шаг интегрирования, соответствующие минимальной и максимальной скоростям открытия (закрытия) регулирующих клапанов.
Уставку Pт0 можно изменять по некоторому закону в функции времени.
4.3.4. Уточнение модели комплексной нагрузки при использовании уточненных моделей генераторов и их систем регулирования достигается детализацией моделей отдельных потребителей и главным образом асинхронных двигателей, которые могут описываться дифференциальными уравнениями, учитывающими электромагнитные и электромеханические переходные процессы (см. гл. 6).
4.3.5. Строгий учет влияния успокоительных контуров синхронных машин в электромеханическом переходном процессе возможен только при использовании уравнений Парка-Горева. Для приближенных уравнений этот учет сводится к вычислению асинхронных мощностей генераторов Pас и дополнительных тормозных моментов ΔР, возникающих при резких изменениях режима. Простейшей оценкой этих факторов служит введение в уравнение движения синхронной машины соответствующих слагаемых
. (4.10)
4.3.6. В тех случаях, когда генераторы представлены неизменной переходной ЭДС , а нагрузки - постоянными полными сопротивлениями (т.е. электрическая сеть описана собственными и взаимными проводимостями генераторов, включающими в себя сопротивления
), асинхронная мощность может быть вычислена по соотношению [Л.3]
, (4.11)
где собственная асинхронная мощность i-го генератора
;
ki - частотный регулирующий эффект нагрузки в i-м узле.
Составляющая Pас(ii) учитывает изменение мощностей нагрузок от частоты; средняя асинхронная мощность от взаимного скольжения между генераторами i, j выражается формулой
,
гдe Mac(i) = f(sij) берется из кривой среднего асинхронного момента генератора при номинальном напряжении. Для исследований динамической устойчивости достаточно иметь начальный участок кривой до значений s < 0,1.
4.3.7. Дополнительное торможение при КЗ вблизи шин генератора наиболее упрощенно можно оценивать по формуле [Л.3].
, (4.12)
где Uг - напряжение на шинах генератора до КЗ;
хвн - электрическая удаленность генератора от точки КЗ;
τа - постоянная времени цепи статора при замкнутой цепи ротора.
Необходимо иметь в виду, что при несимметричных, а также удаленных от шин генератора трехфазных КЗ влияние указанного тормозного момента на изменения угла δ невелико. Для более строгого учета влияния успокоительных контуров можно преобразовать уравнения Парка-Горева с использованием сверхпереходных параметров и получить связь между сверхпереходными ЭДС и проекциями напряжения генератора на оси d, q:
(4.13)
4.4. Применение ЦВМ для расчетов динамической устойчивости
4.4.1. Исследования динамической устойчивости отдельного генератора, группы генераторов или узла нагрузки в простых схемах на аналоговых машинах и электродинамических моделях целесообразно выполнять по специально разработанным экспериментальным программам узкого назначения, составление и отладка которых не должны требовать больших трудозатрат. Могут быть также использованы эталонные программы. При этом необходимо иметь в виду, что те и другие программы, как правило, не содержат достаточного количества средств автоматизации и сервисных подпрограмм обработки исходных данных и результатов расчета. Это может увеличить трудозатраты в случае проведения больших серий расчетов.
4.4.2. Для расчетов динамической устойчивости сложных энергосистем необходимо применять программы расчета электромеханических переходных процессов, образующие единый комплекс с программами расчета установившегося режима и считывающие с внешних запоминающих устройств ЦВМ параметры элементов схемы замещения и параметры режима, проверяемого на устойчивость, см., например, [Л.59]. В результате обеспечивается значительное сокращение трудозатрат и исключается появление ошибок по сравнению с ручной подготовкой указанной информации. Разработанные программы для ЦВМ второго и третьего поколений предназначены главных образом для исследования устойчивости при эксплуатации энергосистем, когда имеется необходимое количество достоверной исходной информации. Эффективность этих программ при выполнении проектных расчетов проявляется в меньшей степени.
4.4.3. Указанные программы предусматривают выполнение расчетов с непосредственным выходом на пульт ЦВМ инженера или оператора, знакомого со спецификой и возможностями программ, который может контролировать ход расчета и при необходимости вмешиваться в него, особенно на этапах начальных расчетов установившегося режима и динамической устойчивости. Возложение этой работы на операторов, не знакомых со спецификой расчетов и особенностями программ, ведет к значительному перерасходу машинного времени и увеличение сроков выполнения исследования. Последующие этапы расчетов можно проводить методом операторского счета при условии продуманной и тщательной организации расчетов.
4.4.4. При выборе тех или иных программ и использовании их для конкретного исследования динамической устойчивости электрической системы необходимо учитывать особенности реализованных в них алгоритмов и методик.
4.4.5. Увеличение отрезка времени, в течение которого рассматривается электромеханический переходный процесс, даже при использовании точных методов численного интегрирования, требует правильного выбора шага интегрирования, особенно в том случае, когда метод не предусматривает оценки накапливающейся погрешности. На этот выбор, с другой стороны, влияет и уточнение моделей генераторов и нагрузок, с которым связано появление малых постоянных времени, например успокоительных контуров ротора и звеньев систем регулирования синхронных машин. В любом случае следует исходить из приближенной оценки шага интегрирования Δt = 0,2T, где T - наименьшая из постоянных времени.
4.4.6. Выполняя проектные исследования динамической устойчивости с помощью ЦВМ, необходимо выполнять пробный расчет для каждого расчетного случая с целью получения информации о степени напряжения в нагрузочных углах. Это даст возможность уточнить способ представления нагрузок в основных расчетах [Л.60, 61].
4.4.7. Следует обращать внимание на организацию выдачи информации об электромеханическом переходном процессе. С увеличением числа генераторов и нагрузок снижается наглядность графической информации, резко возрастает объем табличного материала и тем самым затрудняется анализ и обработка результатов. Применяемые в настоящее время программы не содержат специальных подпрограмм для систематизации, обработки или преобразования информации об электромеханическом переходном процессе в удобную для анализа форму.
Целесообразно осуществлять подробную выдачу только в нескольких начальных расчетах, после выполнения которых можно уточнить и сократить объемы требуемой информации для дальнейших расчетов.
Глава 5. РЕЗУЛЬТИРУЮЩАЯ УСТОЙЧИВОСТЬ ЭНЕРГОСИСТЕМ
5.1. Основные положения
5.1.1. В зависимости от причины и характера нарушения устойчивости системы и других факторов следует различать:
- продолжительный асинхронный режим, для ликвидации которого потребуется разделение системы на отдельные несинхронно работающие части;
- кратковременный асинхронный режим, завершающийся ресинхронизацией.
В последнем случае считается, что в системе обеспечивается результирующая устойчивость [Л.1, 10, 11] . Во многих случаях самопроизвольная ресинхронизация после нарушения устойчивости происходит без применения каких-либо специальных мероприятий и устройств автоматики [Л.62-64]. Этому способствует ряд факторов, основными из которых являются: асинхронные и синхронные моменты вращения генераторов, средства автоматического регулирования возбуждения и скорости вращения агрегатов, автоматическая частотная разгрузка системы и т.п.
5.1.2. В тех случаях нарушения устойчивости, когда предел передаваемой мощности по линии в послеаварийном режиме ниже мощности, передававшейся по электропередаче в нормальном режиме, для обеспечения результирующей устойчивости следует проверить эффективность специальных мероприятий по ограничению величины передачи мощности по линии. При этом нужно учитывать, что, если в переходном процессе после нарушения устойчивости произойдет временная ресинхронизация, то вслед за этим синхронизм вновь будет нарушен, как только передача мощности по линии превысит значение предела статической устойчивости. Для обеспечения результ