РД 34.20.578

МИНИСТЕРСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ СССР

ГЛАВНОЕ ТЕХНИЧЕСКОЕ УПРАВЛЕНИЕ ПО ЭКСПЛУАТАЦИИ ЭНЕРГОСИСТЕМ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ПО ОПРЕДЕЛЕНИЮ УСТОЙЧИВОСТИ ЭНЕРГОСИСТЕМ

Часть II

РД 34.20.578-79

УДК 621.311.019.34 (083.96)

Подготовлены ВНИИЭ, МЭИ, ВГПИиНИИ Энергосетьпроект, ЦДУ ЕЭС СССР, ИЭД АН УССР и НИИПТ: введение - ВНИИЭ, ЦДУ ЕЭС СССР, ИЭД; гл. 1 - ВНИИЭ, ЦДУ ЕЭС СССР; гл. 2 - МЭИ, Энергосетьпроект, ВНИИЭ; гл. 3 - МЭИ, Энергосетьпроект; гл. 4 - МЭИ, Энергосетьпроект; гл. 5 - ВНИИЭ, МЭИ; гл. 6 - ВНИИЭ, МЭИ; гл. 7 - ВНИИЭ, НИИПТ, ЦДУ ЕЭС СССР; гл. 8 - МЭИ; гл. 9 – ИЭД; гл. 10 - ВНИИЭ, ЦДУ ЕЭС СССР; приложения - ВНИИЭ, МЭИ, Энергосетьпроект, НИИПТ, ИЭД.

Составители д-р техн. наук Л.Г. МАМИКОНЯНЦ (введение, гл. 1, 5-7, 10), канд. техн. наук Л.М. ГОРБУНОВА. (гл. 6), канд. техн. наук Ю.Е. ГУРЕВИЧ (гл. 6, приложения 1, 11, 12), инж. Л.Е. ЛИБОВА (гл. 2) канд. техн. наук В.Ф. ТИМЧЕНКО (гл. 7), д-р техн. наук А.А.ХАЧАТУРОВ (гл. 5, 8, приложения 1, 8, 9), ВНИИЭ; д-р техн. наук В.А. ВЕНИКОВ (гл. 2-6, 8, приложение 1), канд. техн. наук Н.Д. АНИСИМОВА (гл. 3, 8, приложения 3, 4, 14), д-р техн. наук Л.А. ЖУКОВ (гл. 2, 5), д-р техн. наук И.В. ЛИТКЕНС (гл. 3, приложения 5, 6), канд. техн. наук В.Д. СТРОЕВ (гл. 3, 6, приложение 10), канд. техн. наук Д.А. ФЕДОРОВ (гл. 4, 5), канд. техн. наук А.Н. ЦОВЬЯНОВ (гл. 4), МЭИ; д-р техн. наук Д.И. АЗАРЬЕВ (гл. 2-4), инж. Ю.А. КИШКИН (гл. 2, приложения 2, 18). инж. Ю.В. МОРОШКИН (гл. 3), инж. Ю.А. ПОЗДНЯКОВ (гл. 3, 4, приложение 7), канд. техн. наук З.Г. ХВОЩИНСКАЯ (гл. 2, приложение 18), инж. Л.П. ШИПУНОВА (гл. 2), Энергосетьпроект; д-р техн. наук C.А. COBАЛOB (введение, гл. 1, 7, 10, приложение 1), канд. техн. наук М.Г. ПОРТНОЙ (гл. 7, 10), ЦДУ ЕЭС СССР; д-р техн. наук Л.В. ЦУКЕРНИК (гл. 9, приложения 15, 16, 17), ИЭД; канд. техн. наук Е.А. МАРЧЕНКО (гл. 7, приложение 13), канд. техн. наук В.А. АНДРЕЮК (гл. 7, приложение 13), НИИПТ.

Редакционная коллегия:

Д.И. АЗАРЬЕВ, В.А. ВЕНИКОВ, Л.Г. МАМИКОНЯНЦ, С.А. СОВАЛОВ, А.А.ХАЧАТУРОВ

Методические указания предназначены для специалистов проектных институтов и эксплуатирующих организаций Минэнерго СССР.

Все замечания и предложения по Методическим указаниям направлять по адресу: 103074, Москва, К-74, Китайский пр., д. 7, Главное техническое управление по эксплуатации энергосистем Минэнерго СССР.

Глава 6. УСТОЙЧИВОСТЬ НАГРУЗКИ

6.1. Статическая устойчивость нагрузки

6.1.1. В качестве основного фактора, определяющего статическую устойчивость нагрузки, следует рассматривать наличие в составе комплексной нагрузки вращающихся машин-асинхронных и синхронных двигателей, что в определенных условиях может приводить к лавине напряжения*. Такая неустойчивость проявляется, в первую очередь, в снижении напряжения на шинах узла нагрузки (до 30-60 % нормального рабочего напряжения), что приводит к нарушению электроснабжения всех потребителей данного узла.

Условия устойчивости нагрузки существенно зависят от характеристик узлов нагрузки энергосистемы и от параметров всей электрической системы в целом. Опасность возникновения лавины напряжения возрастает при увеличении суммарной мощности асинхронных двигателей в составе комплексной нагрузки, их загрузки, электрической удаленности узла от генерирующих источников. Нарушение статической устойчивости нагрузки может проявляться как в энергосистемах, содержащих длинные и относительно короткие, но сильно загруженные линии электропередачи, так и в концентрированных энергосистемах, характеризующихся малой удаленностью электрических станций от центров потребления.

_________________

* В тех случаях, когда лавина напряжения может иметь место, она возникает, если напряжение в узле понижается до значения Uкр, которое называется критическим.

6.1.2. Расчеты устойчивости нагрузки следует проводить для определения запасов устойчивости в нормальных и послеаварийных режимах, а также проверки устойчивости послеаварийных режимов. Запас устойчивости (KU) определяется в соответствии с соотношением

,                                                      (6.1)

где U0 - нормальное напряжение.

6.1.3. При выполнении расчетов, связанных с глубокими понижениями напряжения в узлах нагрузки, нужно иметь в виду, что по ряду причин (в частности, из-за того, что применяемые в настоящее время магнитные пускатели самопроизвольно отключаются при напряжении 0,6-0,8 Uном) снижения напряжения могут вызвать самоотключения потребителей. Сброс нагрузки промышленных предприятий может достигать, по экспериментальным данным, 50 %. Поэтому при выполнении расчетов для действующих энергосистем следует при снижении напряжения на шинах потребителей примерно до 0,7 Uном и ниже учитывать самоотключения, для чего необходимо уменьшать величину двигательной нагрузки на 20÷30 % (ориентировочно).

Поскольку в будущем следует ожидать усовершенствования коммутационной аппаратуры низкого напряжения и улучшения средств защиты и автоматики на промышленных предприятиях, проектные (перспективные) расчеты целесообразно выполнять и без учета самоотключений двигателей.

6.1.4. Для определения критического напряжения и запаса устойчивости нагрузки необходимо осуществлять утяжеление исходного нормального режима. Способы утяжеления режима могут быть различны:

1) снижение ЭДС источников питания при неизменной схеме внешней сети;

2) изменение схемы внешней сети (отключение некоторых элементов), изменение внешнего реактивного сопротивления при ЭДС, равных или отличающихся от ЭДС исходного режима;

3) увеличение активной и реактивной нагрузки узла.

6.1.5. На основании этих расчетов в случае необходимости следует выбирать мероприятия, улучшающие устойчивость нагрузки: регулирование возбуждения синхронных машин, а также отключение части неответственной нагрузки при снижении напряжения в узлах.

Если эти мероприятия не решают задачи, то может быть поставлен вопрос об улучшении характеристик комплексной нагрузки (например, замена части асинхронных двигателей синхронными), а также параметров внешней сети (увеличение мощности питающих трансформаторов, строительство новых линии электропередач в распределительных сетях и т.д.).

6.1.6. При выполнении расчетов устойчивости нагрузки следует учитывать, что неполнота исходных данных (главным образом, в отношении параметров режима двигателей при пониженном напряжении) может решающим образом повлиять на точность расчетов. Если значение критического напряжения оказывается близким к предельно возможному (значение KU≈0,25 - ориентировочно), то следует повторить расчеты, уточнив расчетную модель узла нагрузки. Для этого следует рассчитать более подробную схему распределительной сети с более подробным учетом электроприемников. Может также оказаться необходимым учет условий самораскачивания и влияния на устойчивость нагрузки способов стабилизации АРВ станций энергосистемы. При возможности обязательно проводится экспериментальное определение устойчивости нагрузки.

6.1.7. Общий метод исследования статической устойчивости нагрузки. При использовании метода малых колебаний следует учитывать специфику рассматриваемой задачи. Она заключается в том, что при составлении дифференциальных уравнений, описывающих переходный процесс в энергосистеме, выделяются мощные узлы нагрузки, в то время как остальные узлы нагрузки задаются в виде постоянных сопротивлений.

6.1.8. Нагрузки выделенных узлов следует учитывать статическими характеристиками, представляющими зависимости потребляемой мощности от напряжения на шинах узла U, т.е. Рн= f1 (U), Qн = f2 (U). Синхронные или асинхронные двигатели следует по возможности учитывать в виде отдельных эквивалентных двигателей, подключенных к шинам узла нагрузки.

6.1.9. Уравнения переходных процессов в малых отклонениях для энергосистемы произвольной конфигурации, содержащей n электростанций (представленных эквивалентными генераторами) и m выделенных узлов нагрузки, записываются в следующем виде [Л.1]:

1) Уравнения переходных процессов в эквивалентных генераторах энергосистемы

   (6.2)

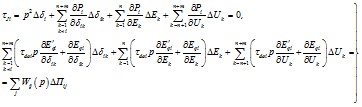
где i = 1, 2, ..., n;

Uk - напряжение k-го узла нагрузки;

Ek - ЭДС генератора*;

δik - угол между векторами и (или и );

Wij(p) - передаточная функция АРВ генератора i по параметру регулирования Пij (см. гл. 3);

р - оператор дифференцирования,

_______________

* Обычно принимают Ek = Еqk, но может быть принято Ek = ЕQk или ; выбор той или иной ЭДС определяется удобством выполнения расчетов и, не влияя на конечные результаты анализа устойчивости, приводит к изменению выражений для частных производных в (6.2) и их численных значений.

2) Уравнения балансов мощностей в узлах нагрузки

;              (6.3)

;            (6.4)

где , - соответственно активная и реактивная мощности, подтекающие от энергосистемы к узлу i (i = n+1, …, n+m);

Pнi, Qнi - мощности составляющей нагрузки узла i, заданной статическими характеристиками;

Pci, Qci - мощности эквивалентного синхронного двигателя узла нагрузки i;

;

;

Рaci, Qaci - мощности эквивалентного асинхронного двигателя узла нагрузки i;

;

,

si - скольжение асинхронного двигателя.

3) Уравнения переходных процессов в эквивалентных двигателях узлов нагрузки.

Синхронные двигатели:

         (6.5)

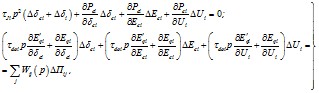
где δci - угол между векторами ЭДС двигателя и напряжения узла;

δi - угол вектора относительно синхронной оси (i = n+1, …, n+m).

Асинхронные двигатели:

.                                            (6.6)

С помощью приведенных уравнений анализ статической устойчивости энергосистемы с учетом характеристик нагрузки можно выполнять любыми известными методами с применением алгебраических или частотных критериев устойчивости.

6.1.10. Анализ статической устойчивости энергосистемы можно существенно упростить, если предположить, что нарушение устойчивости происходит апериодически, без самораскачивания. Последнее обычно имеет место в тех случаях, когда причиной неустойчивости системы является неустойчивость нагрузки, проявляющаяся в виде апериодического процесса - лавины напряжения. В этих случаях условием устойчивости системы является положительность свободного члена характеристического уравнения (an > 0).

В общем случае условие an > 0 является необходимым, но недостаточным условием статической устойчивости и дает несколько завышенные значения пределов устойчивости. Однако погрешность при таком упрощенном подходе будет тем меньше, чем лучше осуществлена стабилизация энергосистемы путем соответствующего выбора структуры и параметров АРВ синхронных машин.

Проведение упрощенных расчетов устойчивости, без учета самораскачивания, позволяет сократить необходимый объем более точных расчетов.

6.1.11. Практические методы расчетов устойчивости нагрузки. Их применение позволяет еще более упростить расчета статической устойчивости нагрузки без снижения и точности по сравнению с расчетом свободного члена характеристического уравнения (см. гл. 3).

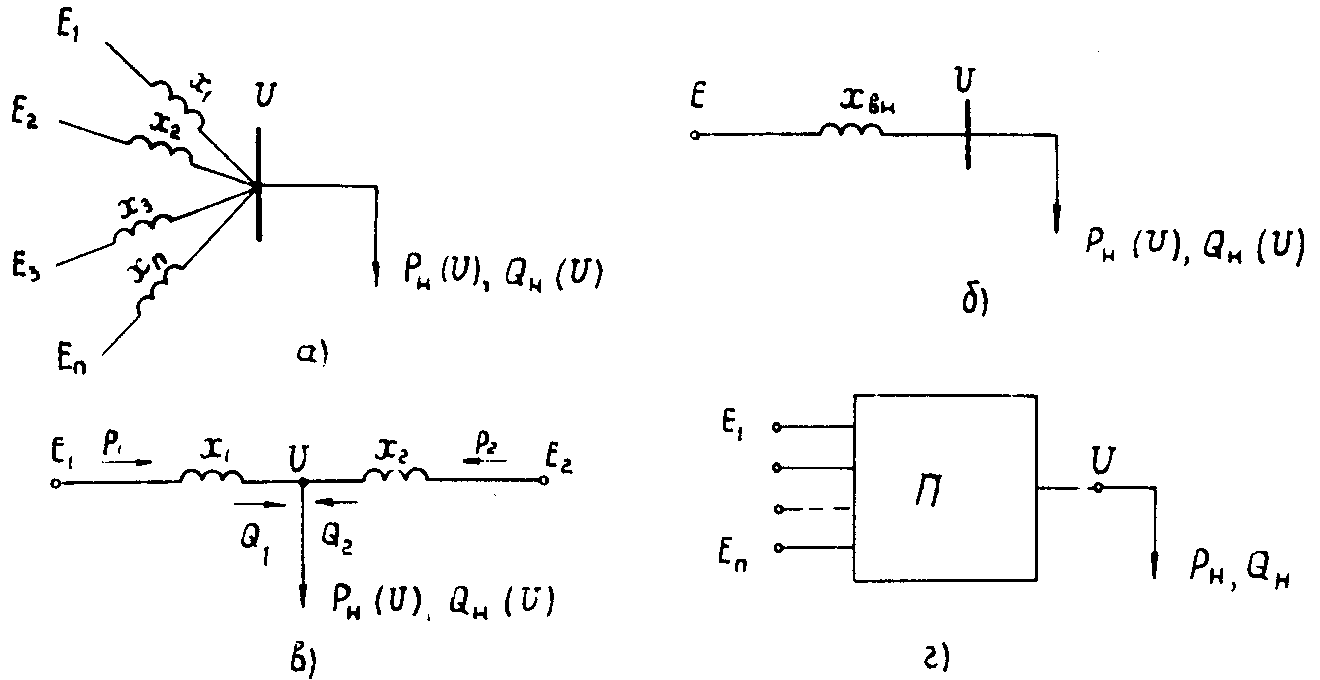
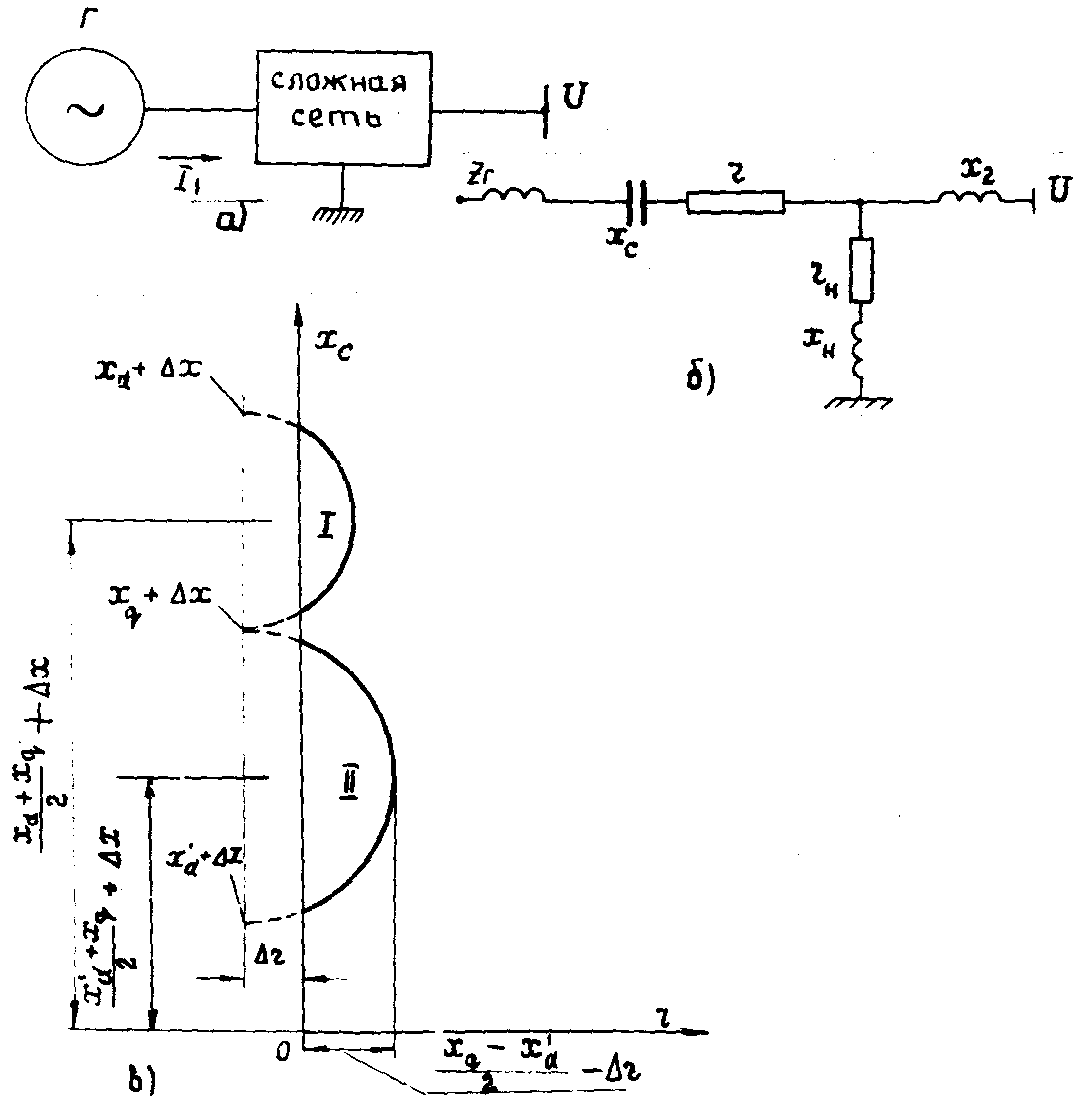
Рис. 6.1. Возможные схемы замещения внешней сети при расчетах статической устойчивости нагрузки:

а - общий вид многолучевой звезды; б - простейшая схема; в - двухлучевая схема;

г – многополюсник

6.1.12. Выбор того или иного практического критерия, из которых наиболее распространенными являются

, ,                                                        (6.7)

следует производить, исходя из соображений простоты и удобства анализа [Л.2]. Эти критерии дают те же результаты, что и расчет an при условии, что энергосистема устойчива при закреплении напряжения в узловой точке (при U = Const).

______________

* ΔQ - это разность между мощностью, притекающей в узел нагрузки от источника питания Qг(U), и мощностью, потребляемой в узле нагрузки Qн (U): ΔQ = Qг (U) - Qн (U).

6.1.13. Анализ статической устойчивости с помощью практически критериев (6.7) для схем, показанных на рис. 6.1, а-в, может выполняться без применения вычислительных или моделирующих устройств и обычно проводится графическим способом в связи с тем, что статические характеристики нагрузок, как правило, задаются таблично или графически. Методика анализа состоит в том, что для ряда значений напряжения в окрестности точки U = U0, соответствующей исходному режиму, устойчивость которого исследуется, строится зависимость либо ΔQ = f (U), либо Ei = φi (U),

где i - номер ветви схемы. Угол наклона касательной к этой кривой в точке U = U0 и определяет условие устойчивости энергосистемы.

6.1.14. При определении зависимости ΔQ = f (U) следует рассчитывать Qi = fi (U), i = 1, 2, …, n, исходя из условия

Ei = Const и , .

6.1.15. Отличие методики расчета Ei = φi (U) от ΔQ = f (U) состоит в том, что появляющийся при изменении U небаланс реактивной мощности (ΔQ) относят на генератор i, что и вызывает изменение его ЭДС Ei.

6.1.16. Определение запаса статической устойчивости исследуемого режима энергосистемы при применении практических критериев проводится так же, как и при применении критерия аn>0 т.е. для каждого режима энергосистемы, определяемого выбранным способом подхода энергосистемы к пределу устойчивости, следует заново рассчитывать зависимости Ei = φi (U) или ΔQ = f (U).

6.1.17. Для оценки значения запаса устойчивости может быть применена более простая методика, состоящая в том, что расчет кривой ΔQ = f (U) или Ei = φi (U) соответствующих исходному режиму энергосистемы, продолжается при уменьшении U вплоть до достижения точки экстремума: dΔQ / dU = 0 или dEi / dU = 0. Напряжение, соответствующее этой точке, будет минимально допустимым с точки зрения статической устойчивости - критическим напряжением Uкр.

Подход к предельному режиму в этом случае для разных критериев будет различным. При применении критерия dΔQ / dU < 0 утяжеление исходного режима энергосистемы состоит в том, что в узел системы подключается дополнительная реактивная нагрузка, равная для каждого значения напряжения узла U = U0 небалансу реактивной мощности (ΔQн = ΔQ), причем : dΔQн / dU = 0 для каждого значения U. При применении критерия dEi / dU > 0 утяжеление исходного режима системы состоит в уменьшении напряжения в узловой точке из-за снижения ЭДС генератора i.

Следует учитывать, что в общем случае значения коэффициента запаса по напряжению KU зависят от применяемого критерия, однако различия обычно не велики.

Задачу определения значения Uкр с помощью указанных критериев можно еще более упростить, полагая, что активная мощность нагрузки, а следовательно, и генераторов энергосистемы, остается постоянной при изменении напряжения в узловой точке. Погрешность от такого упрощения (оцениваемая по значению критического напряжения в узле нагрузки Uкр) тем меньше, чем меньше регулирующий эффект активной мощности нагрузки по напряжению ∂P/∂U. Как показали проведенные расчеты, при ∂P/∂U = 0,6 (что характерно для узлов промышленной нагрузки), эта погрешность не превышает 2-3 % и обычно вполне допустима. Кроме того упрощенные расчеты дают завышенные значения Uкр.

6.1.18. При расчетах статической устойчивости нагрузки схема эквивалентируется и приводится к одному из видов, показанных на рис. 6.1. Аналитические расчеты устойчивости нагрузки следует проводить для схем, показанных на рис. 6.1, а, б, в. Для более сложных схем (рис. 6.1, г) расчеты следует выполнять с помощью ЦВМ.

6.1.19. Следует помнить, что эквивалентирование генераторов в аналитических расчетах устойчивости нагрузки (определение критического напряжения на нагрузках) приводит к правильным результатам только в тех случаях, если фазы ЭДС генераторов совпадают или близки между собой. В остальных случаях эквивалентирование приводит к снижению Uкр, т.е. дает завышенные запасы устойчивости. Однако в большинстве случаев эквивалентирование генераторов не приводит к существенному снижению критического напряжения (см. приложение 10).

6.1.20. При нескольких источниках питания определение критического напряжения при снижении ЭДС источников питания проводится аналогично предыдущему критерию dEi / dU > 0 при заданном изменении ЭДС. Например, при поддержании постоянными ЭДС n-1 источников и заданном распределении между ними активных мощностей постепенным снижением ЭДС n-го источника находится минимальное напряжение, при котором существует режим Pн (U) и Qн (U). Это напряжение и является критическим для данных условий работы энергосистемы.

6.1.21. Проверка устойчивости узла нагрузки по критерию dΔQн / dU < 0 при задании ЭДС источников питания E1, ..., Еn и заданном распределении между ними активных мощностей осуществляется путем построения характеристики QгΣ (U) и сопоставления ее с известной характеристикой нагрузки Qн (U).

Для построения характеристики QгΣ (U) на расчетном столе переменного тока в узле нагрузки устанавливается активный шунт r, соответствующий активной мощности нагрузки Рн (U) (сопротивление шунта меняется в зависимости от напряжения в узле) и некоторый индуктивный шунт х, значение которого в значительной мере определяет напряжение в узле. Изменяя сопротивление r в зависимости от U для различных значений х, добиваются изменения напряжения в узле в широком диапазоне. Потребление реактивной мощности индуктивным шунтом х в зависимости от U и дает характеристику реактивной мощности, притекающей от всех n генераторов (QгΣ). Пересечение QгΣ (U) и Qн (U) определяет исследуемый режим, по dΔQ/dU определяются условия устойчивости нагрузки.

6.1.22. В случае, когда расчеты статической устойчивости нагрузки ведутся для суммарных статических характеристик узла Pн (U) и Qн (U) по практическим критериям, нарушение устойчивости означает нарушение устойчивости узла целиком, без учета отдельных потребителей, хотя во многих случаях нарушение устойчивости отдельных потребителей происходит раньше, чем всего узла нагрузки. Для исследования устойчивости какого-либо элемента он должен быть выделен со своими характеристиками.

6.1.23. При наличии одного источника питания (см. рис. 6.1, б) расчеты по практическим критериям выполняются аналитически следующим образом.

а) Нагрузка задана статическими характеристикам Pн (U), Qн (U). При применении критерия dE / dU > 0 рассчитывается ЭДС энергосистемы в зависимости от напряжения в узле нагрузки

.                                (6.8)

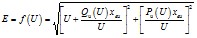
Критическое напряжение Uкр и критическая ЭДС определяются минимумом этой характеристики (dE / dU = 0). Если целью расчетов является проверка устойчивости режима при изменениях внешнего сопротивления хвн и неизменной ЭДС (E = Const), например при исследованиях устойчивости послеаварийных режимов, то целесообразно проверять устойчивость по критерию dΔQ / dU < 0. Для этого в узле нагрузки при выбранном значении хвн и для ряда значений U рассчитывается значение ΔQ

.                       (6.9)

Исходный режим соответствует условию ΔQ = 0. В окрестности рабочей точки определяется знак dΔQ / dU; если dΔQ / dU < 0, то режим устойчив; если dΔQ / dU > 0 режим неустойчив.

Аналогично выполняется расчет для случая роста нагрузки. Тогда при использовании критерия dΔQ / dU < 0 в выражении (6.9) варьируется не значение хвн, а характеристики Рн (U), Qн (U). При этом принимается, что при всех значениях U значения Рн и Qн увеличиваются в одно и то же число раз. В простейших расчетах значение Рн принимается неизменным при изменениях напряжения и росте реактивной нагрузки.

Примеры расчетов устойчивости нагрузки приведены в [Л.3].

б) Нагрузка представлена одиночным асинхронным двигателем.

Критическое напряжение одиночного асинхронного двигателя1, работающего на шины неизменного напряжения, определяется в соответствии с критерием dP / ds [Л.1, 4], как

,                                                          (6.10)

где Р - мощность, потребляемая асинхронным двигателем из электросети2.

_______________

1 В расчетах статической устойчивости предполагается, что значение момента сопротивления на валу двигателя не зависит от частоты вращения. Сопротивление КЗ .

2 В относительных единицах номинальная активная мощность двигателя равна cos φном.

При работе асинхронного двигателя через внешнее сопротивление хвн значение критической ЭДС определяется по формуле

,                                                    (6.11)

а критическое напряжение

,                                                  (6.12)

в) Нагрузка представлена синхронным двигателем. Критическое напряжение одиночного синхронного двигателя, работающего на шины неизменного напряжения, определяется в соответствии с критерием dP / dδ > 0 [Л.1, 4], как

,                                                           (6.13)

где для нерегулируемого двигателя Eдв = Eq, xдв = xd,

для двигателя с АРВ Eдв = E', xдв = x'd.

При работе синхронного двигателя через внешнее сопротивление хвн значение критической ЭДС системы определяется по формуле

,                                                     (6.14)

6.1.24. Определение устойчивости узла нагрузки, имеющего n асинхронных двигателей1, можно выполнить исходя из того, что двигатели одновременно достигают критического скольжения. При этом значения критических напряжений и ЭДС получаются с запасом.

Если в узле нагрузки подключено несколько асинхронных двигателей, питающихся через внешнее сопротивление от энергосистемы с ЭДС Е, то их устойчивость определяется аналогично устойчивости одиночного двигателя. Для этого рассчитывается эквивалентное сопротивление электросети для каждого двигателя , , …, на основании соотношения

,                         (6.15)

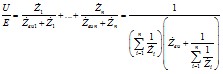
где , …, - сопротивления двигателей;

- эквивалентная проводимость всех двигателей, подключенных к шинам;

,                                                      (6.16)

При расчетах эквивалентного сопротивления в значении сопротивлений двигателя2 подставляются значения критического скольжения sкр.

______________

1 Используются материалы исследований, выполненных И.А. Сыромятниковым.

2 Определение Zi при критическом скольжении дает значения Uкр и Екр с запасом, так как на самом деле критическое скольжение при наличии внешнего сопротивления меньше номинального критического скольжения и, кроме того, не все двигатели одновременно имеют критические скольжения.

По известному эквивалентному сопротивлению для каждого двигателя определяются критическое напряжение Uкp и критическая ЭДС Eкр по уравнениям (6.11) и (6.12) в предположении, что все остальные двигатели работают устойчиво.

После определения критических напряжений и ЭДС (Uкрi и Eкрi) для всех двигателей, они располагаются в порядке уменьшения их критических ЭДС. Пусть для первого двигателя критическая ЭДС равна Екр1. При ЭДС выше, чем Екр1, все двигатели работают устойчиво. После опрокидывания первого двигателя критическая ЭДС второго и всех остальных увеличивается, так как сопротивление первого двигателя становится (s1 = 1). Поэтому для каждого i-го двигателя по уравнениям (6.11) и (6.12) критические напряжения и ЭДС определяются при условии, что i-1 двигателей опрокинулись (Uкр.i-1 > Uкрi) и их сопротивления (, , …, ) определяются при s = 1, а двигатели от i-го до n-го еще не нарушили свою устойчивость и их сопротивления определяются при критических скольжениях si = sкрi, …, sn = sкрn. Тем самым для i-го двигателя определяются критические напряжения и ЭДС, при которых сохраняется устойчивая работа двигателей от i-го до n-го, когда произошло опрокидывание i-1 двигателей1.

______________

1 В действительности часть двигателей вскоре после опрокидывания будет отключена защитой. Это обстоятельство вводит в такой расчет дополнительный запас. (См. также [Л.5]).

Аналогичным образом определяется минимальное напряжение, при котором возможен пуск к двигателей при работающих n двигателях. Тогда при определении , …, принимается s1 = sкр1, …, sn = sкрn, а для , …, принимается sn+1 = sn+2 = … = sn+к = 1.

6.1.25. Для узлов с преобладающей асинхронной нагрузкой и не содержащих источников реактивной мощности значение критического напряжения может быть упрощенно определено на основании эксперимента по косвенным признакам, без опасности возникновения лавины напряжения. Для этого требуется получить статическую характеристику Qн = f2 (U) при понижении напряжения до той точки, где значение Qн минимально (обозначим это напряжение UминQ). Опыт прекращается, как только значение Qн при понижении напряжения начинает возрастать.

Для указанной нагрузки критическое напряжение определяется по формуле

,                                                   (6.17)

где хвн - эквивалентное сопротивление распределительной сети (от выводов асинхронных двигателей до точки, напряжение в которой не зависит от режима рассматриваемой нагрузки1).

Значение хвн берется в относительных единицах, в которых Uбаз = Uдв.ном; .

6.1.26. Устойчивость нагрузки при пуске крупного двигателя. Пуск крупного синхронного или асинхронного двигателя может вызвать существенное понижение напряжения на шинах нагрузки и даже вызвать нарушение статической устойчивости работавших двигателей. Расчет устойчивости нагрузки может быть выполнен указанными выше способами; удобно применение критерия dΔQ / dU < 0. Запускаемый двигатель учитывается в виде дополнительной нагрузки, имеющей сопротивление для асинхронных двигателей или для синхронных2.

_______________

1 Для решения обратной задачи - определения хвн по известным значениям QминQ и Uкр - выражение (6.17) непригодно, так как не обеспечивает удовлетворительной точности.

2 См. также п.6.2.

6.1.27. Влияние статических конденсаторов на устойчивость нагрузки. При исследовании влияния на статическую устойчивость нагрузки статических конденсаторов, параллельно включаемых в узлах нагрузки, они учитываются изменением реактивной мощности потребителей Q = Qн - U2 / xc. Расчет устойчивости в этом случае проводится так же, как и без статических конденсаторов.

Кроме того расчет устойчивости можно упрощенно провести по схеме, приведенной на рис. 6.1, б, в которую должны быть введены следующие эквивалентные параметры

, .                                             (6.18)

При рассмотрении влияния конденсаторных батарей (КБ) на устойчивость нагрузки в общем случае следует учитывать, что при увеличении генерируемой ими мощности может потребоваться (из-за повышения напряжения) изменение коэффициентов трансформации понизительных трансформаторов.

Нужно различать три случая:

а) КБ на понизительной подстанции устанавливаются для того, чтобы повысить напряжение до номинального; коэффициенты трансформации остаются неизменными. В этом случае запас по статической устойчивости двигателей увеличится;

б) КБ устанавливаются не для повышения напряжения, а для увеличения коэффициента мощности нагрузки; напряжение в точке установки КБ (шины НН понизительной подстанции) восстанавливается понижением ЭДС ближайших генераторов или компенсаторов. В этом случае запас по статической устойчивости нагрузки снижается;

в) КБ устанавливаются также для повышения коэффициента мощности, но напряжение на шинах НН подстанции восстанавливается изменением коэффициента трансформации понизительных трансформаторов этой подстанции. В этом случае (в зависимости от значения внешнего сопротивления) запас по статической устойчивости двигателей может как повыситься, так и понизиться.

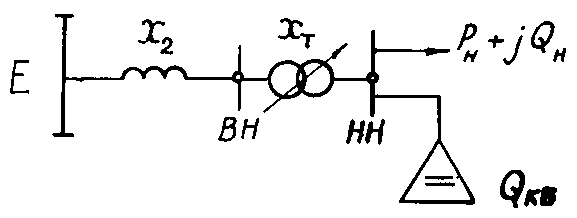
В последнем случае [Л.6] запас по устойчивости двигателей повышается, если сопротивление х2 от шин ВН подстанции до той точки энергосистемы, напряжение в которой не зависит от режима нагрузки (рис. 6.2), больше, чем сопротивление трансформатора хт; если хт > х2, запас по устойчивости двигателей после включения КБ снижается. (Оба сопротивления, разумеется, должны быть приведены к одной ступени напряжения).

В проектной практике расчеты устойчивости с учетом КБ имеют особое значение тогда, когда от решения вопроса о коэффициентах мощности нагрузки зависит выбор мощности трансформаторов, числа цепей и т.п. Неучет влияния КБ в этом случае может привести к тому, что будут получены существенно заниженные значения критического напряжения и, следовательно, в реальных условиях повысится вероятность возникновения лавины напряжения.

6.2. Динамическая устойчивость нагрузки

6.2.1. При анализе динамической устойчивости нагрузки в общем случае следует рассматривать следующие возмущения:

- пуск крупного двигателя;

- автоматическое повторное включение или переключение источников питания (АПВ и АВР), вызванные КЗ в местной электросети;

- КЗ и АПВ в сети высокого напряжения.

Рис. 6.2. Упрощенная схема питания подстанции с конденсаторной батареей

В расчетах учитывается, что за время перерывов питания или понижений напряжения, вызванных КЗ или другими причинами, двигатели тормозятся. Поэтому при восстановлении напряжения двигателя потребляют ток, существенно больший нормального. Это ведет к понижению напряжения в электрической системе и в свою очередь вызывает уменьшение момента вращения двигателей, как тех, которые испытали перерыв питания, так и других, работавших до этого в нормальных условиях. Если не провести соответствующего расчета и не оценить возможного понижения напряжения на выводах двигателей, то может получиться, что после рассматриваемого возмущения электродвигатели не смогут работать: их частота вращения не восстановится, устойчивость нагрузки нарушится. Самозапуск двигателей должен быть осуществлен за время, допустимое по характеру технологического процесса и по нагреву двигателей. Во время самозапуска двигателей в остальной энергосистеме не должно быть таких снижений напряжения, которые могли бы привести к нарушению нормальной работы.

6.2.2. Мощные нагрузки, вызывающие резкие толчки (электрическая тяга, двигатели прокатных станов и др.) требуют при расчетах режимов определения:

- условий, при которых работа этих толчкообразных нагрузок не приводит к недопустимым колебаниям напряжения на остальных нагрузках, например не приводит к нарушению устойчивости других двигателей;

- устойчивости самих двигателей, работавших с переменным моментом.

6.2.3. Помимо указанного, для узлов нагрузки, подключенных к энергосистеме в электрической близости от центра качаний, при возможности возникновения асинхронного режима, следует проверять устойчивость асинхронных и, главным образом, синхронных двигателей при периодических возмущениях, вызванных асинхронным режимом.

6.2.4. Если для конкретного узла нагрузки известны характеристики по напряжению и частоте, то доля двигательной нагрузки в суммарной нагрузке узла определяется, в первом приближении, по формуле

.                                                (6.19)

При расчетах режима нагрузки для неномидальных значений частоты и напряжения можно в качестве первого приближения полагать регулирующие эффекты по напряжению не зависящими от частоты.

6.2.5. Расчеты пуска и самозапуска асинхронных двигателей. Целью расчетов пуска двигателей является:

- определение времени пуска и допустимости нагрева двигателя при пуске;

- проверка, при необходимости, плавности пуска (например для подъемных кранов), постоянства ускорения и других параметров пуска, существенных для технологического процесса;

- оценка влияния понижения напряжения на выводах других потребителей при пуске достаточно мощных двигателей.

В настоящих Методических указаниях рассматривается только последний вопрос, который наиболее существен в маломощных энергосистемах, а также при питании предприятия по линиям электропередачи с недостаточно высокой пропускной способностью, при недостаточной мощности трансформаторов и пр. Наиболее опасным в этом смысле является прямой пуск короткозамкнутых асинхронных двигателей, обычно составляющих основную часть нагрузки. Большой пусковой ток этих двигателей может вызвать снижение напряжения, что приведет к увеличению скольжения остальных работающих двигателей и росту реактивной мощности, потребляемой двигателями. Последнее может привести к опрокидыванию работающих двигателей и к возникновению лавины напряжения.

6.2.6. Задача определения условий самозапуска группы асинхронных двигателей требует в общем случае расчета скольжения для следующих этапов:

- короткое замыкание;

- перерыв питания (бестоковая пауза при АПВ или АВР). Напряжение равно нулю от t = tкз t=tкз + tпер;

- послеаварийный режим; напряжение восстанавливается до уровня, который зависит от токов нагрузки, процессов в генераторах и изменений схемы сети.

Задача расчета пусков двигателей (индивидуальных - в нормальных условиях и групповых - в некоторые случаях при ликвидации отказов) является аналогичной с той лишь разницей, что отдельные этапы расчета могут быть исключены.

6.2.7. Расчеты самозапусков и групповых пусков двигателей обычно преследуют цель определения максимального количества двигателей, для которых возможно восстановление нормального режима за допустимое время. Двигатели, самозапуск которых невозможен, должны своевременно отключаться защитой.

6.2.8. Исходные данные для расчетов пуска и самозапуска асинхронных двигателей следующие:

- схема внешней сети, которая приводится к виду, показанному на рис. 6.3, а, б;

- параметры эквивалентных двигателей (см. приложения 11 и 12);

- статические характеристики по напряжению для прочих потребителей (см. гл. 2).

_______________

1 Одним двигателем могут быть замещены двигатели, которые питаются от одной секции или от секций, находящихся в аналогичных условиях при рассматриваемом возмущении. Следует, однако, избегать эквивалентирования двигателей, имеющих существенно разные зависимости момента сопротивления от частоты вращения (например, поршневые и центробежные компрессоры), а также двигателей, механические постоянные инерции которых различаются более чем вдвое.

6.2.9. Расчет переходного процесса выполняется методом последовательных интервалов. Параметры исходного режима определяются следующим образом:

- схема (см. рис. 6.3) приводится к одному напряжению. Если рассматривается один эквивалентный двигатель, то расчет удобно вести в относительных единицах, принимая для кажущихся мощностей

Sбаз = Sдв.ном.

Независимо от выбора системы единиц для электрического расчета внешней сети, для каждого эквивалентного двигателя вводятся собственные относительные единицы, где Uбазi = Uдв.ном и Sбазi = Sдв.номi, что облегчает расчет скольжений;

- напряжения на шинах потребителей (Uдв) в исходном режиме считаются заданными;

- по известным значениям Рдв = кз cosφном и Uдв по уравнению П.11.2 (см. приложение 11) в собственных относительных единицах определяются скольжения s для исходного режима;

- по выражению (П.11.3) рассчитываются значения реактивных мощностей, потребляемых двигателями, после чего значения Р и Q нагрузок1 пересчитываются к тем абсолютным или относительном единицам, в которых выражены сопротивления сети ("общим" единицам);

________________

1 На этом же этапе учитываются статические потребители своими характеристиками Рст = f1 (U),
Qст = f2 (U).

- рассчитывается ЭДС E (см. рис. 6.3), которая обеспечивает заданное напряжение на шинах потребителей для вычисленных значений активных и реактивных нагрузок.

Таким образом исходный режим, включая начальные скольжения, определен. Далее расчет ведется последовательными интервалами времени с шагом Δt так, чтобы моменты коммутаций совпадали с границами шагов. На каждом шаге выполняются следующие операции:

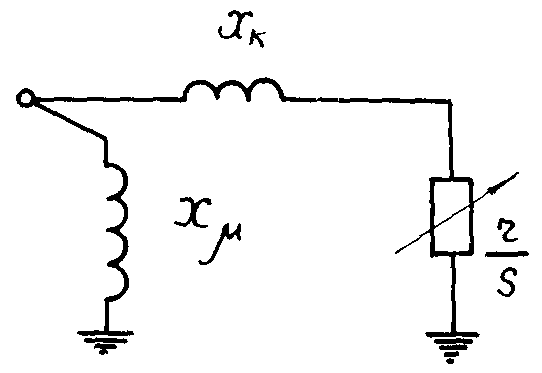
- по известным значениям скольжений рассчитываются параметры схем замещения двигателей (рис. 6.4) и приводятся к «общим» единицам;

- исходя из значения Е, делается электрический расчет схемы для данного режима и определяются значения Uдв. В режиме паузы Uдв = 0;

- до формуле (П.11.2) вычисляются для всех эквивалентных двигателей значения Pдв (в относительных единицах);

- по формуле (П.11.5) вычисляется для известных значений s значения моментов сопротивления;

- определяются скольжения s к концу данного, j-го интервала в предположении, что значения Pдв и Мсопр не изменяются

sj = sj-1 + Δs; .                                     (6.20)

Определяется текущее время к концу данного интервала

tj = tj-1 + Δt.

Далее производится расчет для следующего интервала времени.

Рис. 6.3. Схема сети, внешней по отношению к рассматриваемой нагрузке:

а - общий случай; б – простейшая схема

Рис. 6.4. Г-образная схема замещения асинхронного двигателя

6.2.10. В ряде случаев расчет упрощается. Если в аварийном режиме Uдв = 0, а моментно-скоростная характеристика приводимого механизма выражается квадратичной параболой

Мсопр = кз [mст + (1 - mст) (1 - s)2] cos φном;                                    (6.21)

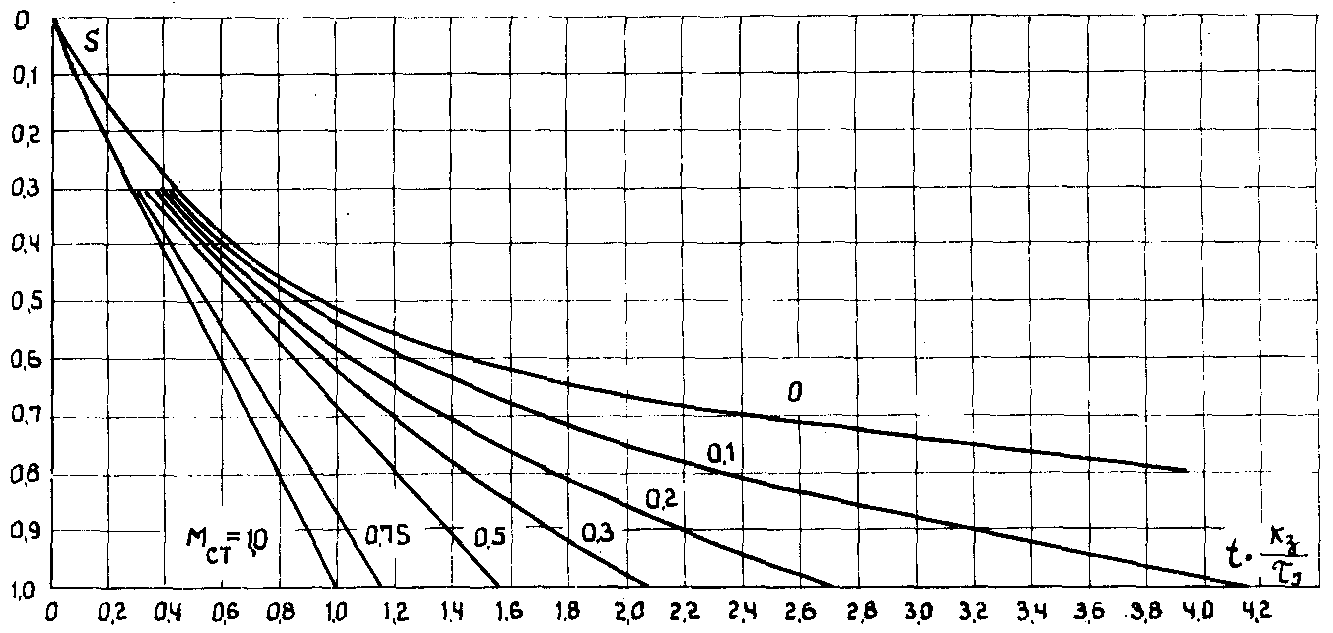
то могут быть использованы кривые выбега, показанные на рис. 6.5, а при mст = 1 и различных значениях остаточного напряжения - кривые на рис. 6.6 [Л.4].

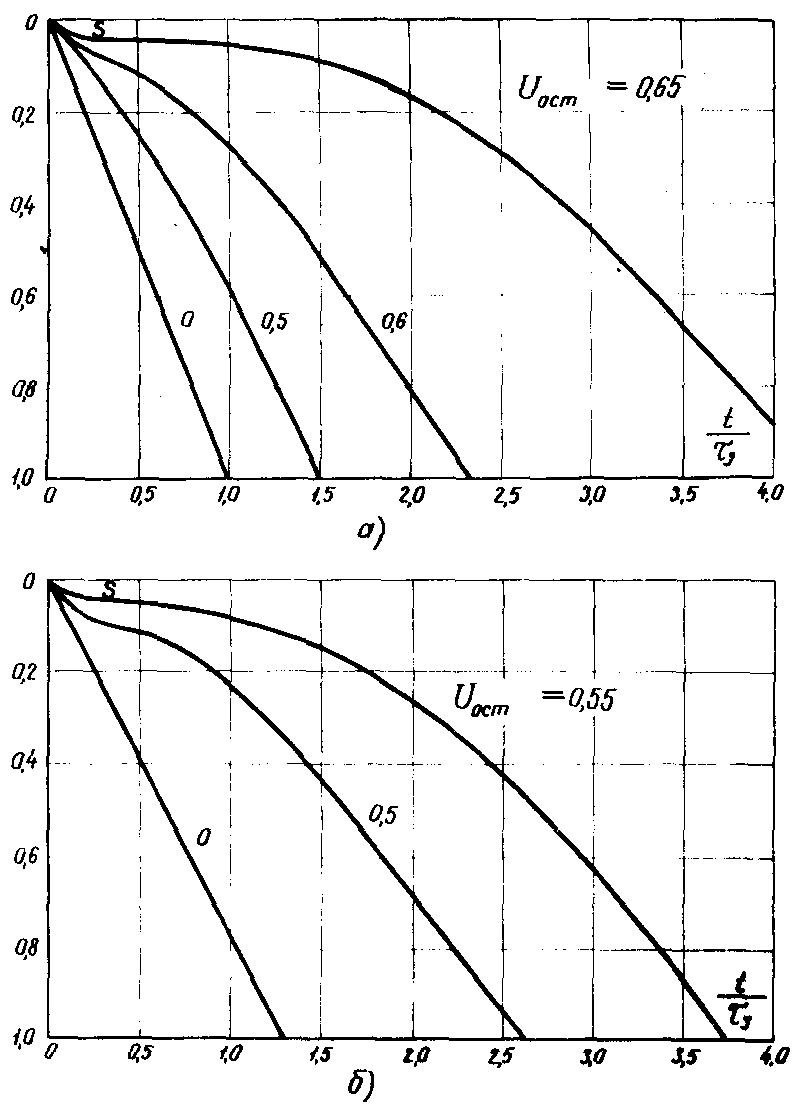
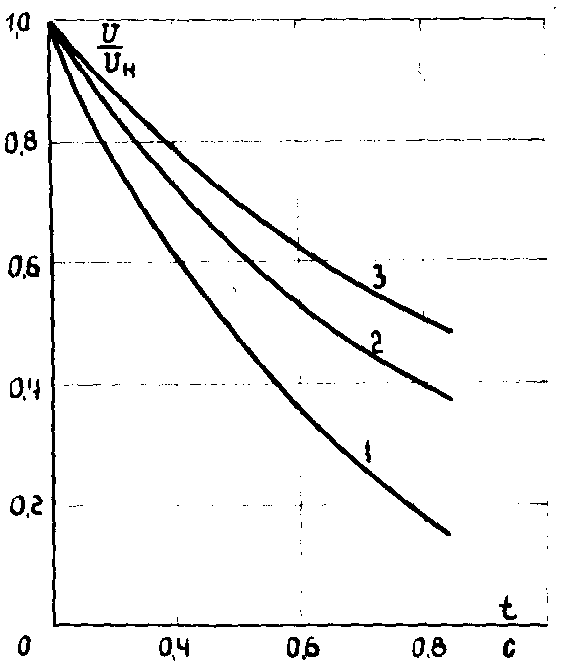
6.2.11. Следует иметь в виду, что при отключении от сети группы асинхронных двигателей (без предшествующего близкого КЗ) электромагнитное поле двигателей исчезает не мгновенно, а с некоторой постоянной времени, достигающей иногда 1 с и более. Кривые затухания напряжения для некоторых условий приведены в качестве примера на рис. 6.71. Из-за наличия остаточного напряжения некоторое время сохраняются взаимные асинхронные моменты двигателей и скольжения двигателей в процессе выбега поддерживаются почти равными, что в приведенной методике расчета не учитывается. За время такого выбега tгр (примерно до Uост = 0,25 Uном).

______________

1 Эффекты, связанные с групповым выбегом при отключении асинхронных двигателей от источника питания (без КЗ), можно не учитывать для мелких двигателей и в тех случаях, когда в составе рассматриваемой нагрузки имеются статические потребители.

;                                                   (6.22)

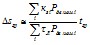
значение tгр определяется по экспериментальной зависимости остаточного напряжения на двигателях от времени, полученной либо для данной, либо для аналогичной в смысле значения 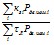группы двигателей.

Если tгр ≥ tпер, то к моменту включения в сеть

;                                                  (6.23)

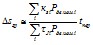
Рис. 6.5. Кривые выбега двигателя при остаточном напряжении равном нулю

Рис. 6.6. Кривые выбега двигателя при различных значениях остаточного напряжения и при постоянном моменте сопротивления:

а - кз = 1,0; б - кз = 0,75

Рис. 6.7. Кривые затухания напряжения на шинах двигателей после их отключения от сети:

1 - группа асинхронных двигателей; 2 - асинхронный и синхронный двигатели; 3 - то же, но синхронный двигатель снабжен АРВ

Если tгр < tпер, то

Δsпер = Δsгр + Δsинд,                                                     (6.24)

где Δsинд - изменение скольжения или при выбеге каждого из двигателей в отдельности (Uост < 0,25) за время Δt = tпер - tгр - определяется как указано выше.

Расчеты пусков двигателей отличаются от описанных тем, что для запускаемых двигателей sнач = 1. Эквивалентная ЭДС Е рассчитывается в предположении, что Uдв = 1, либо перед пуском, либо по окончании пуска, в зависимости от конкретных условий.

6.2.12. Во всех расчетах, связанных с глубокими понижениями напряжения на выводах двигателей, обязателен учет того обстоятельства, что при U < (0,6÷0,8) Uном отпадают контакты магнитных пускателей, что может привести к самоотключению значительной части двигателей низкого напряжения. Отключения двигателей могут иметь место также и от защит минимального напряжения (с соответствующими выдержками времени).

6.2.13. Динамическая устойчивость синхронных двигателей. Расчеты динамической устойчивости синхронных двигателей в общем случае следует выполнять так же, как и для генераторов (см. гл. 4). При рассмотрении вопросов динамической устойчивости двигателей может быть принято Мсопр = Const.

6.2.14. Выбор уравнений синхронных двигателей осуществляется так же, как и для генераторов. Могут быть использованы уравнения Парка-Горева или, если асинхронный режим не рассматривается, то может быть принято допущение о постоянстве ЭДС Е'.

6.2.15. Вели рассматриваемые двигатели имеют АРВ, то последние учитываются соответствующими уравнениями. Релейная форсировка возбуждения учитывается упрощенно: кратностью форсировки и постоянной времени возбудителя.

6.2.16. Асинхронные двигатели целесообразно вводить в расчет их схемой замещения и уравнением движения. Статические потребители в большинстве случаев могут быть представлены постоянными сопротивлениями.

6.2.17. Пуск и самозапуск синхронного двигателя. При наличии в составе нагрузки синхронных двигателей постоянная времени затухания напряжения при перерыве питания (без предшествующего КЗ) может достигать 5 с и более. В таких случаях выбег можно рассчитывать по (6.22).

6.2.18. Расчеты процесса самозапуска, а также пуска синхронных двигателей выполняются аналогично описанному для асинхронных двигателей. Асинхронный момент синхронного двигателя1 может быть вычислен так же, как и для генератора (см. гл. 5). Напряжение на выводах синхронного двигателя в процессе его самозапуска может быть рассчитано при введении в расчетную схему пускового сопротивления . (Существенные уточнения дает только решение уравнений Парка-Горева). Расчет электромагнитной мощности по формуле асинхронного момента дает достаточно точные результаты, если возбуждение отсутствует.

_______________

1 При расчете асинхронного момента учитывается, в соответствующих случаях, увеличение реактивных сопротивлений при непрямом пуске двигателя и активного сопротивления цепи возбуждения, если обмотка ротора замкнута на гасительное сопротивление.

6.2.19. При наличии возбуждения следует учитывать существенные колебания тока статора и колебания напряжения на выводах двигателя, из-за чего возрастают потери в статоре двигателя (иногда более чем на 20%) и уменьшается средний асинхронный момент. В качестве одной из основных мер облегчения самозапуска следует рассматривать гашение поля двигателя при перерывах питания.

6.2.20. Если рассчитывается самозапуск или пуск одиночного двигателя, то достаточно сопоставить асинхронную характеристику при вычисленном значении Uдв с моментно-скоростной характеристикой приводимого механизма Мсопр = f (s)* и найти скольжение sуст, которое установится в конце самозапуска. Если в переходном процессе участвует несколько двигателей, в том числе асинхронных, изменение частоты которых может существенно повлиять на уровни напряжения, то расчет ведется методом последовательных интервалов, как описано выше, вплоть до скольжения sуст.

_____________

* В моменте сопротивления Мсопр при расчете самозапуска синхронных двигателей следует учесть тормозной момент двигателя

,

где rст - сопротивление в цепи статора.

6.2.21. Возможность ресинхронизации синхронного двигателя определяется сравнением скольжения, которое может установиться после окончания самозапуска (sуст) со скольжением втягивания (sвт). Ресинхронизация обеспечивается (при наихудших условиях), если

,                                              (6.25)

где М - максимальный синхронный момент двигателя по отношению к источнику питания с учетом значения Е и внешнего сопротивления (см. гл. 5), отн. ед.;

τJ - постоянная инерции двигателя, с;

Iв - ток возбуждения, зависящий от системы регулирования возбуждения.

Из формулы (6.25) следует, что при форсированном возбуждении ресинхронизация облегчается. Для облегчения как ресинхронизации, так и самозапуска, используют также (при возможности) временное снижение механического момента сопротивления.

6.3. Устойчивость двигателей при асинхронном режиме в энергосистеме

6.3.1. Если рассматриваемый узел нагрузки питается от точки энергосистемы, расположенной в электрической близости от центра качаний, то возникающие при асинхронном режиме периодические колебания напряжения и частоты могут явиться причиной нарушения устойчивости как синхронных, так и асинхронных двигателей.

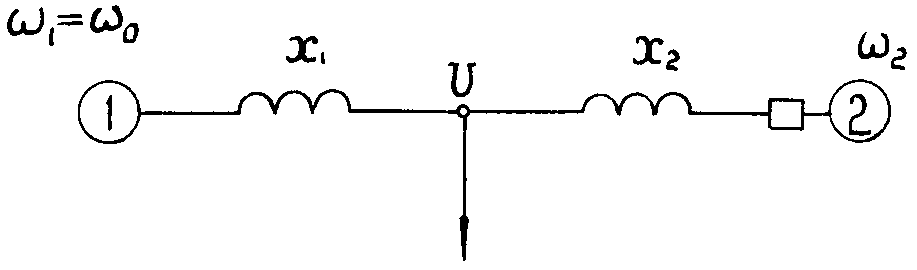
Целесообразно рассматривать схему, в которой две части энергосистемы связаны через сопротивление х = х1 + х2. За сопротивлением х1 от первого генератора расположен узел нагрузки (рис. 6.8). Электродвижущие силы обоих генераторов могут быть представлены постоянными по модулю значениями . Векторы и вращаются с относительным скольжением s, соответствующим разности частот в асинхронно идущих частях энергосистемы. Напряжение в узле нагрузки (если сопротивление узла велико по сравнению с сопротивлением между энергосистемами) определяется как

;                                          (6.26)

фаза напряжения в узле изменяется по закону

.

Рис. 6.8. Схема для расчета условий питания нагрузки при асинхронном режиме в энергосистеме

6.3.2. Устойчивость двигателей в условиях асинхронного режима в энергосистеме в общем случае следует проверять как при возникновении асинхронного хода, так и при установившемся асинхронном ходе.

6.3.3. Переходный процесс, обусловленный возникновением асинхронного режима в энергосистеме, может представить опасность главным образом для синхронных двигателей при следующих условиях:

а) если асинхронный режим возникает в результате несинхронного включения (НАПВ или включение при установившейся разности частот);

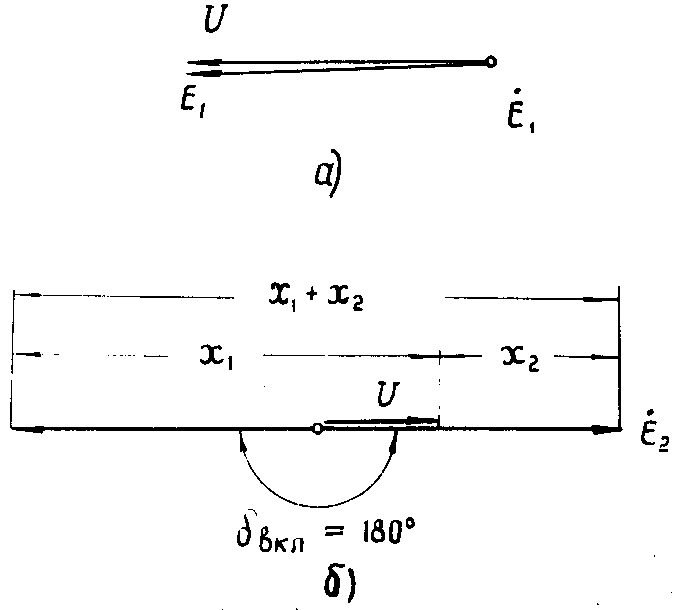
б) если до несинхронного включения нагрузка питалась со стороны энергосистемы 1 и если x1 > x2 (см. рис. 6.8). Тогда при включении энергосистем в противофазе фаза напряжения в узле нагрузки может изменяться скачком на 180° (см. векторную диаграмму на рис. 6.9). В этом случае двигатель оказывается в генераторном режиме, что обычно вызывает нарушение его устойчивости.

6.3.4. Во время асинхронного хода между энергосистемами 1 и 2 может произойти нарушение устойчивости как синхронных, так и асинхронных двигателей вследствие понижения среднего уровня напряжения, а также (для синхронных двигателей) в результате раскачивания при резонансе.

6.3.5. Для проверки устойчивости двигателей в указанных режимах схема энергосистемы, по отношению к рассматриваемому узлу нагрузки, приводится к виду, показанному на рис. 6.8. Определяются возможные случаи несинхронных включений. Если возможен случай, показанный на рис. 6.9, б, то делается вывод о том, что имеется вероятность1 нарушения устойчивости синхронных двигателей. На рис. 6.10 приведена достаточно характерная кривая вероятности сохранения устойчивости синхронным двигателем, построенная при условии, что включения с любыми углами равновероятны. Ресинхронизация таких двигателей наступает обычно по окончании асинхронного хода и проверяется по формуле (6.25).

_______________

1 Вероятность нарушения устойчивости определяется вероятностью включения с углами, близкими к 180°, и мало зависит от параметров двигателя и параметров асинхронного режима.

Рис. 6.9. Векторные диаграммы для случая включения энергосистемы 2 при x1 > x2:

а - до включения; б - в момент несинхронного включения

Рис. 6.10. Пример вероятности сохранения динамической устойчивости синхронного двигателя при несинхронном включении в энергосистеме

6.3.6. Для установившегося асинхронного режима при допущении, что ЭДС энергосистем 1 и 2 равны единице, определяется глубина периодических понижений напряжения

.                                                          (6.27)

Если

,                                                        (6.28)

то устойчивость асинхронного двигателя сохраняется при любой разности частот между энергосистемами. Если

,                                                     (6.29)

то устойчивость нарушается всегда.

Если

,                                             (6.30)

то устойчивость асинхронных двигателей сохраняется в некотором диапазоне разности частот между энергосистемами и постоянных инерции двигателей; определение этого диапазона следует провести с помощью ЦВМ.

6.3.7. Условия устойчивости синхронных двигателей существенно зависят от резонансных явлений и поэтому для оценки этих условий требуются расчеты по уравнениям Парка-Горева с помощью вычислительных средств. Такие расчеты позволяют найти пределы устойчивости асинхронных и синхронных двигателей при асинхронном режиме в энергосистеме и определить такую продолжительность асинхронного режима, при котором не успевает произойти нарушение устойчивости.

6.3.8. Если схема энергосистемы такова, что при асинхронном режиме нарушается устойчивость ответственных потребителей, а мероприятия, повышающие устойчивость нагрузки (АРВ двигателей, отключение части нагрузки и т.д.) оказываются неэффективными, то следует рассмотреть вопрос об ограничении продолжительности асинхронного режима или об отказе от НАПВ.

Глава 7. УСТОЙЧИВОСТЬ СЛАБЫХ МЕЖСИСТЕМНЫХ СВЯЗЕЙ

7.1. Общие указания

7.1.1. При расчетах режимов линий электропередач, используемых в качестве межсистемных связей, следует учитывать нестабильность передаваемой мощности из-за случайных колебаний нагрузки в соединяемых энергосистемах и значительные изменения среднего значения обменной мощности при непредвиденных изменениях баланса мощности в соединяемых энергосистемах.

Имеющие случайный характер колебания обменной мощности заставляют выбирать расчетную (плановую) нагрузку межсистемных связей с больший запасом по статической устойчивости, чем при стабильной передаваемой мощности. Эти колебания зависят от мощности соединяемых энергосистем и сказываются на передаваемой мощности в тем большей степени, чем меньше отношение предела по статической устойчивости межсистемной связи к мощности меньшей из соединяемых энергосистем, т.е. чем более "слабой" является межсистемная связь1. Для слабых межсистемных связей нерегулярные колебания оказывают значительное влияние на режим работы связей и существенно ограничивают использование их пропускной способности.

________________

1 В [Л.7] к слабым связям отнесены связи, для которых отношение предела по статической устойчивости к мощности меньшей из соединяемых энергосистем не превышает 0,1-0,15. Эти значения могут быть приняты для энергосистем относительно небольшой мощности.

7.1.2. Допустимо полагать, что с ростом мощности энергосистемы абсолютные величины нерегулярных колебаний нагрузки возрастают примерно пропорционально корню квадратному из суммарной нагрузки энергосистем, а относительные величины нерегулярных колебаний (отнесенные к мощности энергосистемы) соответственно уменьшаются. В общем случае слабыми рекомендуется считать связи, для которых отношение предела по статической устойчивости к суммарной мощности меньшей из соединенных энергосистем не превышает: 0,15-0,1 - при мощности энергосистемы до 3000 МВт; 0,1-0,08 - при 3000-10000 МВт; 0,08-0,05 - при 10000-30000 МВт; 0,05-0,03 - при 30000-60000 МВт.

Изменения обменной мощности приводят к необходимости оперативной корректировки режима для поддержания среднего значения обменной мощности на заданном уровне и для предотвращения опасных для устойчивости перегрузок межсистемной связи.

7.1.3. По способу регулирования передаваемой мощности следует различать связи:

а) с ручным регулированием, по которым средние значения передаваемой мощности периодически корректируются оперативным персоналом;

б) с автоматическим регулированием (ограничением) передаваемой мощности.

7.1.4. При определении запасов устойчивости межсистемных связей должна учитываться нестабильность передаваемой мощности и отклонения этой мощности от заданного (планового) значения, которые имеются при ручном регулировании и не могут быть полностью устранены при автоматическом регулировании.

7.1.5. Следует учитывать структуру межсистемных связей. Межсистемная связь может состоять как из одиночной линии электропередачи, так и из ряда линий, в том числе с промежуточными нагрузками и электростанциями относительно небольшой мощности. Межсистемная связь без промежуточных электростанций называется межсистемной связью простой структуры, при наличии таких электростанций - межсистемной связью сложной структуры.

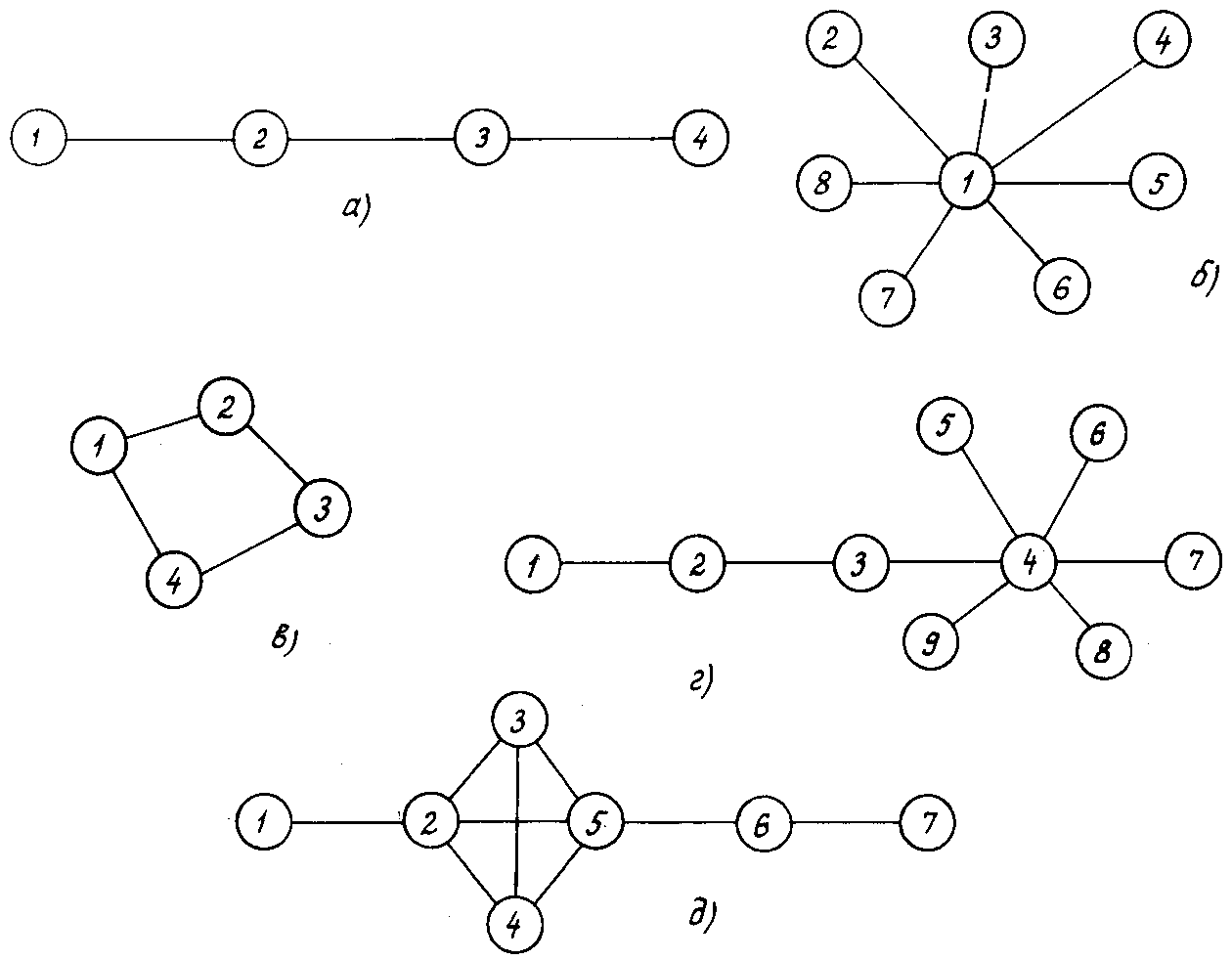
Объединенные энергосистемы с несколькими межсистемными связями могут иметь различную конфигурацию. Из всей совокупности различных схем можно выделить ряд наиболее распространенных, приведенных на рис. 7.1.

7.1.6. В тех случаях, когда несколько концентрированных энергосистем соединяются слабыми связями, следует различать независимые и зависимые слабые связи [Л.8]. Слабые связи можно считать независимыми, если каждая из них соединяет только две энергосистемы, и число слабых связей на единицу меньше, чем число соединяемых энергосистем. В противном случае слабые связи являются зависимыми.

Если слабые связи независимы, то взаимные мощности между энергосистемами, непосредственно между собой не соединенными, имеют значения на 1-2 порядка меньше, чем взаимные мощности между энергосистемами, непосредственно соединенными слабыми связями. Такое различие взаимных мощностей объясняется шунтирующим действием промежуточных энергосистем. Примером независимых слабых связей могут служить связи в схемах, представленных на рис. 7.1, а, б, г. Примеры схем с зависимыми слабыми связями показаны на рис. 7.1, в, д.

7.1.7. Наличие концевых энергосистем, мощность которых значительно больше, чем предел устойчивости и максимум передаваемой мощности по связи, вносит ряд особенностей в определение статической и динамической устойчивости, асинхронных режимов и условий ресинхронизации межсистемных линий электропередач.

Рис. 7.1. Характерные структуры энергосистем:

а - цепная; б - многолучевая звезда; в - кольцевая; г, д - различные сочетания

7.2. Особенности расчета статической устойчивости

7.2.1. Для выполнения расчетов статической устойчивости схема межсистемной связи простой структуры должна быть задана реактивными и активными сопротивлениями элементов, входящих в состав связи (линий электропередач и трансформаторов), и величинами отборов мощности. В случае межсистемной связи сложной структуры должны быть заданы также параметры эквивалента генераторов, подключенных в промежуточных точках связи.

7.2.2. В расчетной схеме генераторы, присоединенные в промежуточных точках, замещаются неизменными ЭДС за своими переходными реактивными сопротивлениями. Относительно небольшие (сравнительно с пропускной способностью связи) промежуточные нагрузки в приближенных расчетах могут быть замещены постоянными сопротивлениями. При больших отборах мощности и при проведении уточненных расчетов должны быть учтены статические характеристики нагрузок.

Соединяемые (концевые) энергосистемы замещаются эквивалентными реактивными сопротивлениями КЗ от ЭДС энергосистемы до точек примыкания связи. Неизменные ЭДС за этими реактивными сопротивлениями определяются расчетом исходного режима по напряжению в точке примыкания связи и передаваемой (принимаемой) активной и реактивной мощности.

7.2.3. В тех случаях, когда промежуточные нагрузки замещаются постоянными сопротивлениями, предельная мощность рассчитывается по формулам

                                      (7.1)

для передающего конца и

                                     (7.2)

для приемного конца. Формулы записаны для положительного направления мощности (пере дача из энергосистемы А в энергосистему Б).

7.2.4. Если механическая инерция (или приближенно мощность) энергосистемы А значительно меньше, чем энергосистемы Б, то предел по статической устойчивости совпадает с максимумом мощности в начале связи по статической характеристике зависимости этой мощности от угла по электропередаче. Предельный угол по электропередаче при этом равен 90°+αАБ. При обратном соотношении инерции (мощностей) нарушение статической устойчивости наступает при угле 90° - αАБ, когда достигает максимума мощность в конце связи.

При соизмеримых значениях мощностей энергосистем, предельный угол может быть приближенно определен по формуле

,                                              (7.3)

где K - отношение мощности меньшей энергосистемы А к мощности большей энергосистемы Б.

7.2.5. В случае необходимости учета статических характеристик промежуточных нагрузок, а также для межсистемных связей сложной структуры, расчет предельных по устойчивости режимов производится обычно с помощью ЦВМ.

7.2.6. Установившиеся режимы и статические угловые характеристики мощности для сравнительно несложных схем слабых связей могут быть определены расчетом "вручную". Простейший метод расчета заключается в следующем: проводится расчет нормального исходного режима, определяются параметры режима по концам связи РА, РБ, UA, UБ, ЭДС за реактивными сопротивлениями концевых энергосистем (ЕА, ЕБ) и напряжения в точках присоединения промежуточных нагрузок. Далее (если расчет ведется от приемного конца связи) для каждого нового (большего) значения РБ при неизменной ЭДС ЕБ подбирается такое значение QБ, чтобы, ведя расчет по участкам с учетом характеристик промежуточных нагрузок по напряжению, получить на приемном конце значение ЕА, соответствующее исходному режиму.

7.2.7. При определении предела устойчивости на статической модели или по полученной аналитически статической угловой характеристике мощности следует иметь в виду, что предел устойчивости слабой связи обычно достигается при значении угла, превышающем угол, соответствующий максимуму мощности на приемном конце линии электропередачи. При соизмеримых мощностях концевых энергосистем предельным по устойчивости с небольшим запасом можно считать режим, в котором достигается максимум мощности по приемному концу линии электропередачи.

7.2.8. При значительном изменении промежуточных нагрузок (как это имеет место, например при наличии электротяги) предельная мощность на приемном конце изменяется в широких пределах, а соответствующая предельному режиму мощность на передающем конце изменяется значительно меньше. Вследствие этого задавать предельный режим и запас устойчивости целесообразно по передающему концу линии электропередачи.

7.2.9. В тех случаях, когда не производится специальный расчет надежности, запас статической устойчивости в нормальном режиме определяется в соответствии с [JI.7] по формуле

,                                                        (7.4)

где Рпр - предел по статической устойчивости;

кр - коэффициент запаса по статической устойчивости, который должен быть не менее 20% для нормального режима и 8% для послеаварийного режима;

- передаваемая мощность (среднее значение);

ΔР - увеличение передаваемой мощности, из-за ее нерегулярных колебаний, вызванных колебаниями нагрузки и частоты в соединяемых энергосистемах.

7.2.10. При отсутствии достоверных данных по значениям нерегулярных колебаний мощности межсистемных связей в [JI.7] рекомендовано (при отсутствии автоматического регулирования) принимать значение ΔР равным 2% суммарной мощности генераторов меньшей из соединяемых энергосистем.

Эта рекомендация была основана на опыте эксплуатации регулируемых вручную межсистемных связей, соединяющих энергосистемы средней мощности - порядка 4-6 тыс. МВт. Анализ нерегулярных колебаний мощности в условиях эксплуатация показывает, что для более мощных энергосистем, даже при ручном регулировании, значение ΔР может быть принято меньше 2%.

7.2.11. При наличии экспериментальных данных по статистическим характеристикам колебаний обменной мощности или колебаний частоты в соединяемых энергосистемах величину запаса статической устойчивости целесообразно определять расчетом надежности работы межсистемной связи (см. п. 7.6).

7.2.12. По условиям надежности значение ΔР рекомендуется выбирать такое, чтобы при нормированном запасе по статической устойчивости кр = 20%, нарушения статической устойчивости происходили бы не чаще одного раза в год при условии, что среднее значение передаваемой мощности корректируется персоналам не реже, чем один раз в 20-60 мин.

При отсутствии исходных данных, необходимых для расчета надежности, можно принимать для предварительной оценки следующие значения ΔР в процентах от мощности меньшей из соединяемых энергосистем: для энергосистем мощностью до 3000 МВт ΔР = 2,5%; 3000-6000 МВт ΔР = 2,5-2%; 6000-10000 МВт ΔР = 2-1,5%; 10000-30000 ΔР = 1,5-1%; 30000-60000 ΔР = 1-0,7%.

Эти значения соответствуют приближенной зависимости

,                                                      (7.5)

где Рн - суммарная нагрузка энергосистемы, МВт*.

________________

* В тех случаях, когда внутренние связи в энергосистемах (по соотношению предела статической устойчивости к мощности меньшей из соединяемых энергосистем) являются слабыми, определение дополнительного запаса статической устойчивости этих внутренних связей может производиться подобно тому, как это рекомендовано для межсистемных связей.

Определяемые по формуле (7.5) значения ΔР приблизительно равны утроенному среднеквадратичному отклонению обменной мощности от среднего значения на интервале усреднения 20÷60 мин, определяемом частотой вмешательства персонала, корректирующего среднее значение обменной мощности. Если имеется автоматическое регулирование (ограничение) обменной мощности, то значение ΔР снижается в соответствии с характеристиками регулирования.

7.2.13. Автоматические системы регулирования (ограничители) обменной мощности способны поддерживать на допустимом пределе (с небольшими отклонениями) среднее значение обменной мощности и подавлять нерегулярные колебания, имеющие длительность порядка нескольких минут. Это дает возможность при наличии соответствующих автоматических систем регулирования снижать значение ΔР при обеспечении того же уровня надежности работы межсистемной связи.

Как показывает опыт эксплуатации, существующие автоматические системы регулирования (ограничения) обменной мощности позволяют уменьшить значение дополнительного запаса устойчивости ΔР примерно в 2-2,5 раза по сравнению со значениями, указанными для регулирования "вручную", за счет поддержания постоянным среднего значения перетока и некоторого подавления нерегулярных колебаний с периодами 10 мин и более.

7.2.14. Для нескольких энергосистем, соединяемых независимыми слабыми связями, предел устойчивости каждой из них практически не зависит от мощности, передаваемой по соседней слабой связи, поэтому расчеты статической устойчивости выполняются независимо для каждой слабой связи по формулам (7.1) - (7.2). Значения ΔР определяются по сумме мощностей меньшей части энергообъединения по сторонам рассматриваемого сечения.

7.2.15. Для нескольких энергосистем, соединяемых зависимыми слабыми связями, предел устойчивости по каждой из связей зависит от мощности, передаваемой по соседним связям. В общем случае определение предела по статической устойчивости производится с использованием метода малых колебаний: аналитически для простейших схем или на аналоговых или цифровых вычислительных машинах для более сложных схем.

7.3. Особенности расчета динамической устойчивости

7.3.1. Причинами нарушения динамической устойчивости межсистемных связей могут быть:

- короткие замыкания;

- аварийные небалансы мощности в соединяемых энергосистемах (набросы нагрузки, отключения генераторной мощности);

- асинхронные режимы по соседним линиям электропередачи.

7.3.2. В качестве расчетных для проверки динамической устойчивости рассматриваются КЗ по концам межсистемной связи, а при сложной структуре связей - также и в точках примыкания промежуточных электростанций. Расчет динамической устойчивости межсистемных связей производится с использованием обычных методов (см. гл. 4).

При коротких замыканиях на слабой связи обычно можно считать, что нагрузки в соединяемых этой связью энергосистемах не изменяются. Возможность нарушения динамической устойчивости слабых связей в результате КЗ невелика, так как по этим линиям электропередачи передается небольшая часть мощности соединяемых энергосистем.

7.3.3. Динамическую устойчивость при внезапном изменении мощности в одной из соединяемых энергосистем следует рассматривать с учетом зависимости мощности от частоты для соединяемых энергосистем.

7.3.4. Приближенно можно принимать, что динамическая устойчивость обеспечивается, если, во-первых, обеспечивается динамическая устойчивость в первом цикле качаний при условии постоянства мощности турбин и, во-вторых, обеспечивается статическая апериодическая устойчивость послеаварийного режима с учетом частотных характеристик энергосистем. Для простых случаев (две энергосистемы соизмеримой мощности) могут быть использованы следующие приближенные критерии. Для динамической устойчивости в первом цикле качаний

        (7.6)

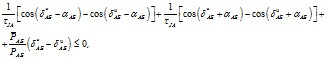
где

                                     (7.7)

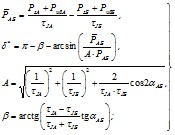
РгА, РгБ - взаимная мощность передающего и приемного концов связи в доаварийном режиме;

τJA, τJБ - средневзвешенные постоянные инерции концевых энергосистем;

- значение угла по электропередаче в доаварийном режиме;

αАБ - угол, дополнительный к углу взаимного сопротивления;

РнбА, РнбБ - значения аварийных выбросов мощности в концевых энергосистемах (положительное значение соответствует увеличению генераторной мощности).

Для статической устойчивости в послеаварийном режиме

,                 (7.8)

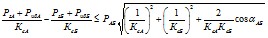
КсА, КсБ - коэффициенты крутизны статических частотных характеристик соединяемых энергосистем (отн.ед.);

Приведенные выше величины (Рг, τг, Рнб, Кс) отнесены к единой базисной мощности.

7.3.5. Расчеты следует выполнять для случаев аварийных снижений генераторной мощности в приемной энергосистеме и аварийного увеличения избытка мощности в передающей энергосистеме.

Если одинаковы постоянные инерции и коэффициенты крутизны статических частотных характеристик, приведенные к номинальной мощности каждой из энергосистем, то может быть использована более простая приближенная формула, полученная так же, как аналогичная формула в [Л.9],

,                                 (7.9)

где ΔРАмакс - максимально допустимое значение наброса мощности в энергосистеме А.

7.3.6. При определении динамической устойчивости расчетное значение перетока должно быть несколько увеличено по сравнению со средним плановым значением для учета влияния нерегулярных отклонений перетока.

7.4. Особенности расчетов ресинхронизации

7.4.1. Условия ресинхронизации слабых связей во многих случаях весьма благоприятны. Ресинхронизация обеспечивается после нарушения динамической устойчивости или несинхронного АПВ при всех режимах, вплоть до близких к пределу устойчивости. Для двух и трех энергосистем можно пользоваться приближенными аналитическими методами, в более сложных случаях - моделированием или расчетом на ЦВМ.

7.4.2. При расчете ресинхронизации слабых связей асинхронный момент не учитывается ввиду его малости по сравнению с остальными демпфирующими моментами (изменением нагрузки и моментов турбин при изменении частоты).

7.4.3. Если две энергосистемы соединяются слабой связью без промежуточных нагрузок с малым активным сопротивлением линии или же с промежуточными нагрузками, но при малых значениях αАБ, предельная по условиям ресинхронизации мощность определяется по следующей формуле [Л.10]

.                                         (7.10)

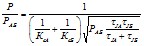
Расчет устойчивости одной из слабых связей (соединяющей энергосистемы А и Б) при асинхронном режиме по соседней слабой связи (соединяющий энергосистемы Б и В) производится следующим образом:

а) по формуле (7.6) или (7.9) определяется устойчивость одной связи при набросе мощности, вызванном нарушением устойчивости другой связи;

б) если разность частот, при которой ресинхронизируется энергосистема В с остальными двумя энергосистемами, меньше, чем частота собственных колебаний связи, соединяющей энергосистемы А и Б, то определяется максимальное отклонение угла ΔδАБмакс при резонансе собственных и вынужденных колебаний

.                                   (7.11)

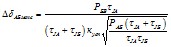
где кусп – коэффициент, определяемый зависимостью нагрузки от частоты и регуляторами скорости турбин. Обычно кусп = 4÷8*.

______________

* Формула (7.11) получена приравниванием энергии, получаемой от энергосистемы В за каждый период асинхронного хода, к той энергии, которая затрачивается на демпфирование при синхронных качаниях энергосистем А и Б [Л.11].

Затем по кривой, показанной на рис. 7.2, определяется снижение предельной мощности , передаваемой по слабой связи, соединяющей энергосистемы А и Б.

Рис. 7.2. Кривая для расчета ресинхронизации по слабой связи

7.4.4. В тех случаях, когда есть промежуточные нагрузки или нельзя пренебречь активными сопротивлениями линий электропередачи, удобнее определять предельный угол исходного режима, при котором обеспечивается ресинхронизация [Л.10]. Формула для определения этого угла имеет следующий вид

           (7.12)

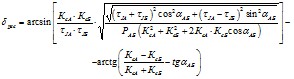
7.5. Особенности расчетов устойчивости с помощью АВМ

7.5.1. Расчеты устойчивости слабых связей на АВМ могут выполняться для определения:

- статической устойчивости в объединенных энергосистемах с зависимыми слабыми связями (т.е. когда число слабых связей равно или больше числа энергосистем);

- динамической устойчивости (в том числе и характера переходного процесса) при отключении части нагрузки или генераторов в одной из энергосистем, затяжном КЗ, отключении одной из слабых связей или при ее асинхронном режиме;

- взаимного влияния процессов, происходящих в одной части энергообъединения на работу других его частей;

- результирующей устойчивости и асинхронных режимов (в том числе и характера переходного процесса) при несинхронном АПВ и нарушений динамической устойчивости;

- эффективности различных автоматических устройств, предназначенных для повышения устойчивости слабых связей.

7.5.2. Для расчета устойчивости слабых связей допустимо моделирование схемы из эквивалентных генераторов по уравнениям движения. Число эквивалентных генераторов должно быть равно числу концентрированных энергосистем, соединяемых слабыми связями.

При моделировании уравнений движения мощно учитывать только те взаимные мощности, которые создаются слабыми связями, соединяющими данные соседние концентрированные энергосистемы. В тех случаях, когда остальные взаимные мощности по крайней мере на порядок меньше, пренебрежение ими практически не влияет на результаты расчета.

7.5.3. Регуляторы скорости эквивалентных агрегатов можно моделировать по наиболее простому уравнению. В ряде случаев переходные процессы на слабых связях происходят настолько медленно, что можно не учитывать инерцию регуляторов скорости.

7.6. Определение надежности режима работы слабых межсистемных связей и методика выбора запасов устойчивости

7.6.1. Надежностью режима работы межсистемной связи называется ее способность обеспечивать продолжительную параллельную работу соединяемых энергосистем без нарушений устойчивости. Одним из существенных факторов, способных оказывать влияние на надежность режима параллельной работы энергосистем, соединяемых слабыми связями, являются превышения предела устойчивости линии электропередачи при нерегулярных колебаниях обменной мощности [Л.8, 9]. Эти превышения и вызываемые ими нарушения синхронизма на слабых связях носят случайный характер. Поэтому задачу оценки надежности режима работы слабых связей в условиях нерегулярных колебаний обменной мощности следует рассматривать как вероятностную*.

________________

* В [Л.12, 13] для решения данной задачи предложено использовать элементы теории случайных процессов. Тем самым задача оценки показателей надежности режима работы слабой связи в условиях нерегулярных колебаний обменной мощности и задача экспериментальной оценки статистических характеристик этих колебаний получили возможность количественного решения.

7.6.2. В качестве основного показателя надежности [Л.12, 13] используется средняя продолжительность безотказной работы - среднестатистическое значение промежутка времени между последовательно возникающими нарушениями устойчивости (отказами в нормальном режиме слабой связи).

7.6.3. Требования к надежности должны основываться на минизации расчетных затрат, т.е. сопоставлении затрат на повышение надежности с достигаемым снижением народнохозяйственного ущерба, вызываемого отказами (нарушениями устойчивости) межсистемной связи. В настоящее время вследствие отсутствия достоверных данных о величине ущерба от нарушений устойчивости такой подход к определению надежности слабых связей неосуществим. Можно считать надежность достаточной, если средняя продолжительность безотказной работы межсистемной слабой связи при плановом потоке мощности составляет не менее одного года*. Для связей, нарушение работы которых не представляет опасности для соединяемых энергосистем, расчетная продолжительность безотказной работы может быть снижена.

_____________

* Имеются в виду отказы, вызванные нерегулярными колебаниями обменной мощности.

7.6.4. С учетом требований надежности коэффициент запаса по статической устойчивости межсистемной связи должен определяться такой величиной, которая отвечала бы определенному уровню надежности. Надежность определяется относительной величиной отстройки среднего значения передаваемой мощности от предела Рпр

,                                                           (7.13)

где σ - среднеквадратическое отклонение нерегулярных колебаний мощности.

7.6.5. Рекомендуются две методики вероятностной оценки надежности режима слабой связи в условиях случайных колебаний обменной мощности: методика НИИПТ [Л.14] и методика ВНИИЭ [Л.15]. Эти методики различаются принимаемой моделью процесса нерегулярных колебаний обменной мощности: в [Л.14] этот процесс моделируется марковским стационарным процессом с нормальным распределением вероятности, а в [Л.15] - гауссовским (нормальным) стационарным случайным процессом. Обе методики дают практически совпадающие оценки среднего времени безотказной работы слабой связи и могут быть использованы как для связей, регулируемых вручную, так и для автоматически регулируемых связей. По [Л.14] эффект автоматического регулирования учитывается на стадии статистической обработки экспериментальных данных по колебаниям обменной мощности.

Рис. 7.3. График функции φ (х) к расчету вероятностной оценки надежности режима слабой связи

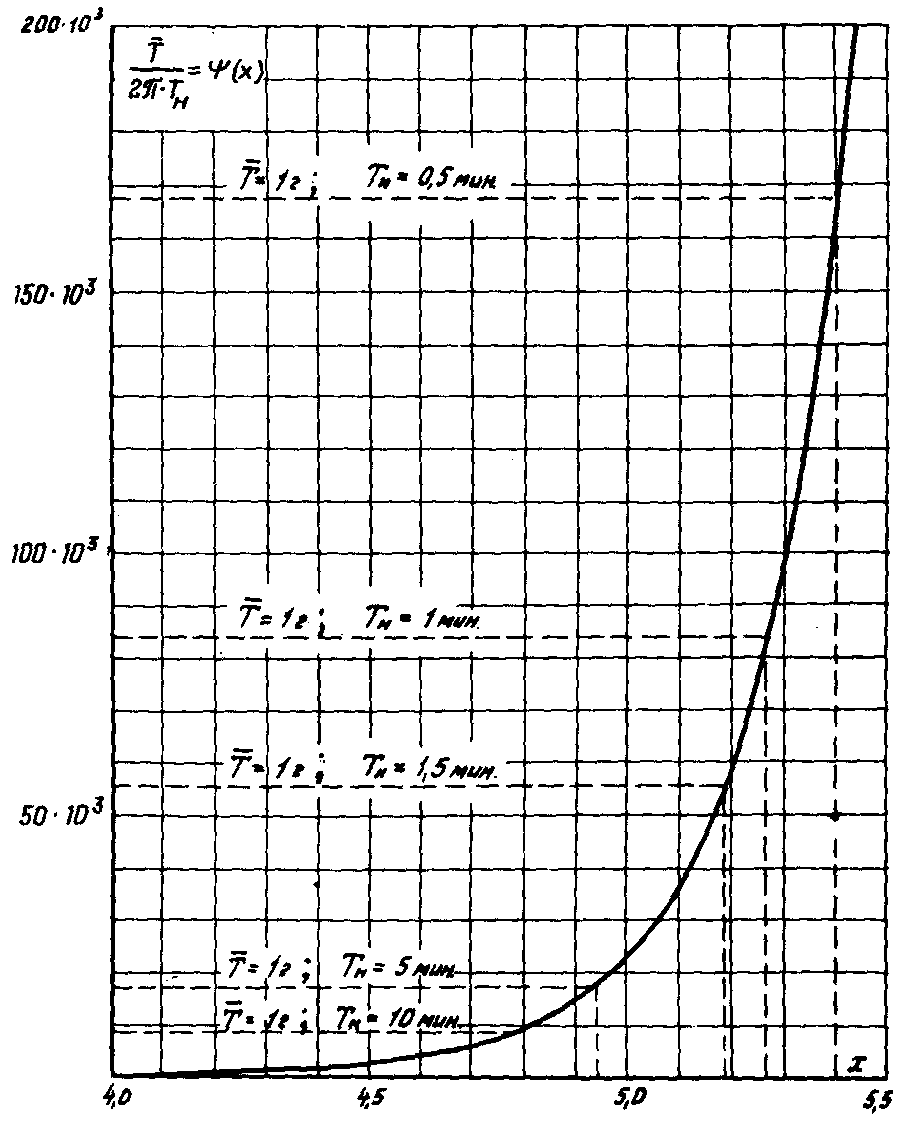
7.6.6. Методика НИИПТ. На рис. 7.3 приведен график функции

,                                                     (7.14)

причем средняя продолжительность параллельной работы энергосистем без нарушения устойчивости связана с функцией φ (x) следующим соотношением

,                                                         (7.15)

где Tp - постоянная времени корреляционной функции Kp (τ) колебаний мощности по межсистемной связи

.                                                        (7.16)

Для того чтобы определить значение , необходимо располагать двумя параметрами корреляционной функции колебаний обменной мощности по связи: среднеквадратическим отклонением нерегулярных колебаний мощности σ и постоянной времени корреляционной функции Тр. При помощи первой из них из выражения (7.13) по заданным значениям предела статической устойчивости Рпр и планируемого среднего значения перетока мощности определяется значение отстройки х. Далее для полученного значения отстройки х из графика рис. 7.3 определяется соответствующее значение функции φ (х), а из выражения (7.15) с помощью второго параметра корреляционной функции Тр определяется значение средней продолжительности безотказной работы.

Для работающих связей параметры корреляционной функции σ и Тр могут быть определены статистической обработкой данных измерений обменной мощности. При решении вопросов присоединения изолированно работающей энергосистемы можно определить параметры корреляционной функции случайных колебаний небалансов активной мощности по измерениям случайных колебаний частоты, учитывая существующую связь между корреляционными функциями частоты (индекс "s") и нагрузки (индекс "н"):

,                                                   (7.17, а)

.                                                     (7.17, б)

.                                                    (7.17, в)

откуда

                                                            (7.18)

здесь Кс - коэффициент крутизны статической частотной характеристики энергосистемы (отн.ед.).

Методика экспериментального определения значений Кс, Ts и σs по регистрациям частоты в энергосистеме изложена в приложении 13. Испытания, проведенные в ряде действующих энергосистем, показывают, что в диапазоне малых отклонений частоты (0,08÷0,12 Гц) значения Кс находятся в пределах 3÷5.

В тех случаях, когда суммарные нагрузки соединяемых на параллельную работу энергосистем различаются более, чем в три раза, можно принимать, что корреляционная функция колебаний обменной мощности по связи совпадает с корреляционной функцией колебаний небаланса активной мощности меньшей из энергосистем, т.е.

                                                              (7.19)

При объединении на параллельную работу энергосистем соизмеримой мощности параметры корреляционной функции колебаний обменной мощности по связи могут быть выражены через параметры корреляционных функций колебаний небалансов мощности систем следующим образом:

,                                                   (7.20)

,                                            (7.21)

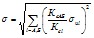
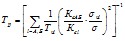
где

,                                                      (7.22)

КсАБ - эквивалентный коэффициент крутизны статической частотной характеристики энергообъединения; А и Б - индексы передающей и приемной энергосистем.

Энергообъединение сложной структуры, когда приемная и передающая его части не являются концентрированными энергосистемами, а содержат, в свою очередь, энергосистемы со слабыми связями, приводится к энергообъединению из двух энергосистем, параметры каждой из которых определяются из выражений

,                                                          (7.23)

,                                                  (7.24)

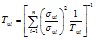
.                                                           (7.25)

Эквивалентные параметры энергообъединения определяются по формулам (7.22)-(7.24). Во всех формулах суммируются величины, приведенные к базисной мощности [Л.14].

В случае применения автоматического регулирования обменной мощности спектр нерегулируемых колебаний небаланса между суммарной нагрузкой и генерацией содержит относительно быстрые и меньшие по величине колебания, что учитывается соответствующим выбором параметров математического фильтра, при помощи которого производится статистическая обработка экспериментальных записей нерегулярных колебаний мощности на ЦВМ (см. приложение 13). Экспериментальные исследования НИИПТ показывают, что для энергосистем мощностью 3÷20 тыс. МВт можно принимать: = 0,2÷0,4%; Тр = 0,5÷2,5 мин; при этом зависимость от значения суммарной нагрузки энергосистемы удовлетворительно аппроксимируется выражением, аналогичным (7.5)

или , МВт.               (7.26)

Из рис. 7.3 видно, что значение запаса, необходимого для обеспечения , равного одному году, при изменении Тр = Тн в пределах 0,5÷1,5 мин изменяется относительно мало и близко к 5σрег, где σрег определяется по формуле (7.26). Поэтому в ориентировочных расчетах можно принимать, что запас устойчивости этих связей на нерегулируемые колебания должен быть порядка х = 5. Вероятность отказа регулятора при этом не принимается во внимание.

7.6.7. Методика ВНИИЭ [Л.15]. Среднее время безотказной работы слабой связи оценивается средним временем между выбросами обменной мощности за относительный уровень (7.15), которое оценивается по следующей формуле

,                                                        (7.27)

где no - среднее в единицу времени (например, за час) число пересечений нерегулярными колебаниями обменной мощности уровня, равного математическому ожиданию процесса на данном интервале усреднения;

Ф (х) - гауссовское (нормальное) распределение вероятности Ф (х) ≈ 1 при х ≥ 2,5.

"Доверительные" оценки σ и no определяются [Л.16] усреднением результатов, полученных на N часовых интервалах (Ти = 1 ч), относящихся к характерным областям суточных графиков нагрузки соответствующей энергосистемы или энергообъединения (10 ≤ N ≤ 25). Кроме того, определяются зависимости σ и no от продолжительности интервала усреднения.

Для Ти = 0,5÷1 ч*

_______________

* По данным экспериментов, выполненных для энергосистем мощностью до 100000 МВт [Л.16, 17].

, МВт                                                   (7.28)

с = 0,40÷0,50,

no = 15÷25 1/час.

Зависимости этих характеристик от продолжительности интервала усреднения следующие: для τи от 10 до 60 мин при Ти = 60 мин

,                                                     (7.29)

.                                                           (7.30)

Зависимость среднего времени безотказной работы (7.27) от величины отстройки (7.13) показана на рис. 7.4. При no = 25 1/ч отстройкам x* = 4,5÷5 соответствует = 1000÷10000 ч. При использовании формулы (7.28) в качестве Рн подставляется значение суммарной нагрузки меньшей из соединяемых энергосистем или группы энергосистем меньшей мощности по одну сторону от рассматриваемой межсистемной связи. Значение коэффициента с зависит от времени суток и характера графика нагрузки. Рекомендовано принимать с = 0,5 для дневных интервалов от начала утреннего подъема до окончания вечернего спада нагрузки, а для остальных часов - с=0,4. При увеличения мощности энергообъединений сверх 50000 МВт значение коэффициента с может иметь тенденцию к некоторому увеличению. Поэтому в условиях эксплуатации целесообразно уточнять этот коэффициент экспериментальным путем для конкретных условий работы.

________________

* По данным экспериментов, выполненных для энергосистем мощностью до 100000 МВт [Л.16, 17].

Рис. 7.4. Зависимость среднего времени безотказной работы в зависимости от величины отстройки, no = 20 1/ч

Указанным значениям отстройки (запаса) в размере (4,5÷5) σ (МВт), где σ определяется формулой (7.28), соответствует оперативная "ручная" корректировка перетока по слабым связям (в часы стабильной нагрузки), которая производится 1-2 раза в час, а в часы подъема и спада нагрузки энергосистем чаще, в соответствии с фактическим ходом изменения перетока и в зависимости от ответственности данной слабой связи в энергообъединении.

7.6.8. Как видно из сопоставления выражений (7.28) и (7.26), автоматическое регулирование межсистемного перетока снижает нерегулярные колебания обменной мощности. Это позволяет увеличить среднюю передаваемую мощность. Однако отказ по каким-либо причинам регулятора перетока приводит к восстановлению колебания обменной мощности до естественных величин и к увеличению вероятности нарушения устойчивости параллельной работы по данной связи. Выбранная с учетом вероятности отказа регулятора отстройка регулируемого перетока по [Л.16] может быть снижена с 5σ до (2-3)σ, где значение σ определено по формуле (7.28). Такая отстройка предоставляет оперативному персоналу время, достаточное для того, чтобы после отказа регулятора вручную снизить переток и сохранить устойчивость.

Таким образом, исходя из принятых требований надежности, определяемых средней продолжительностью безотказной работы , может быть определен расчетный запас статической устойчивости для автоматических регулируемых и регулируемых вручную слабых межсистемных связей.

7.6.9. Полученная из анализа надежности суммарная отстройка среднего перетока от предела статической устойчивости, равная примерно хΣ = 5σ, должна быть сопоставлена с рекомендованным выше запасом статической устойчивости: 3σ плюс нормативный запас 20%. Допустимая средняя (плановая) нагрузка слабой межсистемной связи определяется большим из сопоставленных запасов.

При этой необходимо учитывать, что в нормальном режиме в случаях, когда это необходимо для предотвращения ограничения потребителей или потери гидроресурсов, допускается длительная работа линии электропередачи с уменьшенным до 5÷10% запасом, в зависимости от ее роли в энергосистеме и последствий возможного нарушения устойчивости. При меньшей отстройке перетока требуется его более частая корректировка. Соответственно, в зависимости от характера использования слабой межсистемной связи, времени, в течение которого должна быть увеличена обменная мощность, и последствий возможного нарушения устойчивости, значение также может быть снижено до нескольких месяцев.

7.6.10. Наряду с нерегулярными колебаниями обменной мощности на надежность режима работы межсистемных слабых связей могут оказывать влияние следующие факторы: внезапные отключения мощных источников энергии или нагрузки в соединяемых энергосистемах, отключения участков или параллельных цепей межсистемных линий электропередачи, понижения напряжения по концам межсистемной связи, изменения частоты энергообъединений [Л.9] и т.п. Вопросы учета вероятностей подобных эксплуатационных возмущений при управлении режимами межсистемных линий электропередачи рассматриваются в [Л.18-20]. Методика расчетов надежности с учетом основных влияющих факторов изложена в [Л.21]; эта методика может быть рекомендована пока лишь для опытного применения.

Глава 8. САМОВОЗБУЖДЕНИЕ И САМОРАСКАЧИВАНИЕ В ЭНЕРГОСИСТЕМАХ

8.1. Общие указания

8.1.1. Под самовозбуждением следует понимать вид электромагнитной неустойчивости генераторов, при появлении которой в значительной степени или полностью теряется возможность управления установившимся режимом. При этом в отдельных точках системы самопроизвольно могут устанавливаться значения напряжений, опасные для изоляции оборудования. Нарастание тока и напряжения в процессе самовозбуждения может быть либо апериодическим (синхронное самовозбуждение), либо колебательным (асинхронное самовозбуждение). Частота тока и напряжения при самовозбуждении соответствует частоте собственных колебаний в электрическом контуре, образованном внешней сетью с входным емкостным сопротивлением, и электрической машиной. Амплитуда собственных колебаний ограничивается насыщением стали машин и трансформаторов.

Асинхронное самовозбуждение является наиболее опасным для электрических систем вследствие того, что колебания тока и напряжения нарастают до максимального значения в течение нескольких периодов, а существующие автоматические регуляторы возбуждения не в состоянии подавить этот быстроразвивающийся процесс.

8.1.2. Точное определение условий, при которых возможно появление самовозбуждения, следует выполнять анализом системы линейных неоднородных дифференциальных уравнений для вращающейся машины и внешней сети, содержащей емкость. Для нахождения соотношений параметров машины и внешней сети, при которых возможно появление самовозбуждения, а также мероприятий, устраняющих это явление, насыщение может не учитываться [Л.22-30].

8.1.3. Под самораскачиванием следует понимать вид электромеханической периодической неустойчивости энергосистемы, при которой ротор синхронной машины совершает самопроизвольные колебания, заканчивающиеся либо выпадением машины из синхронизма, либо установлением какого-то предельного цикла колебаний, препятствующих нормальной работе энергосистемы. Самораскачивание - явление редкое в практике работы энергосистем и может появиться у небольших слабо загруженных синхронных и асинхронных машин, работающих на сеть со значительным активным сопротивлением, когда отрицательный демпферный момент может быть существенным.

Применение продольной емкостной компенсации на дальних линиях электропередачи, установка компенсированных емкостью синхронных компенсаторов, сооружение электропередач, настроенных на полуволну, повышает вероятность возникновения самораскачивания.

8.1.4. Аналитическое исследование самораскачивания может быть достаточно полно проведено с помощью уравнений Парка-Горева, записанных для малых колебаний энергосистемы в любом заданном нагрузочном режиме.

При принятых условиях энергосистему можно считать линейной и использовать для анализа линеаризованные уравнения Парка-Горева в приращениях значений тока, потокосцепления, угла и т.д.

8.1.5. Самораскачивание и самовозбуждение могут проявляться совместно. Тем не менее, проверку энергосистемы на отсутствие самовозбуждения и самораскачивания проводят раздельно, так как при реальных постоянных инерции роторов машин начало развития самовозбуждения происходит практически при неизменной частоте вращения ротора.

8.2. Самовозбуждение в простейшей энергосистеме

8.2.1. В процессе проектирования и эксплуатации энергосистем следует определять соотношения параметров цепи машина - емкостная нагрузка1, при которых возникает самовозбуждение.

Рис. 8.1. Схема замещения к расчету самовозбуждения

8.2.2. Во многих случаях схему рассматриваемой части энергосистемы можно приводить к виду, показанному на рис. 8.1; в этой схеме синхронная машина работает на шины неизменного напряжения (в частном случае U = 0) через емкостное сопротивление хс, внешние индуктивное и активное сопротивление r.

_____________

1 Емкостной нагрузкой может быть, например линия электропередачи, включенная односторонне на один или несколько генераторов станции.

* Индуктивное сопротивление хвн, если иное специально не оговорено, вводится в сопротивление машины xd, xq, и т.д.

8.2.3. Возможность возникновения самовозбуждения (необходимое условие) определяется наличием правых корней в характеристическом уравнении [Л.1].

a0 pn + a1 pn-1 + … + an-1 p + an = 0,                                        (8.1)

что имеет место, согласно критерию Гурвица, при соблюдении неравенств:

                                                               (8.2)

где Δn-1 - предпоследний определитель Гурвица, составленный из коэффициентов (8.1).

Процесс самовозбуждения будет развиваться (достаточное условие), если точка, координаты которой характеризуются параметрами внешней сети хс и r, располагается внутри одной из зон самовозбуждения (рис. 8.2). При этом границы зон самовозбуждения [Л.22, 31] следует определять из условий:

an = 0                                                                    (8.3)

для зоны I синхронного самовозбуждения и

Δn-1 = 0                                                                  (8.4)

для зон II, III асинхронного самовозбуждения.

Рис. 8.2. Зоны самовозбуждения явнополюсной синхронной машины

8.2.4. Возможность возникновения синхронного самовозбуждения, при котором частота свободных колебаний в цепи статора равна синхронной частоте, следует учитывать как при замкнутой, так и при разомкнутой обмотке возбуждения.

8.2.5. Зона I синхронного самовозбуждения в координатах r и x ограничена половиной окружности, центр которой расположен на оси xс и сдвинут на (xd + xq) / 2 относительно начала координат. Указанная полуокружность (рис. 8.2) пересекает ось ординат в точках xc1 = xd и xc2=xq, т.е. при r = 0 зона синхронного самовозбуждения определяется значениями емкостного сопротивления внешней сети согласно неравенству

xq < xc < xd.                                                               (8.5)

Радиус окружности, которая получается по условию (8.3), определяет максимальное значение активного сопротивления, при котором возможно появление синхронного самовозбуждения:

.                                                           (8.6)

При наличии в системе активного сопротивления r > rмакс синхронное самовозбуждение невозможно.

8.2.6. Возможность возникновения асинхронного самовозбуждения в зонах II* и III, где частота вращения ротора не равна частоте колебаний в контурах статора, следует учитывать лишь при замкнутой обмотке возбуждения при изменении емкостного сопротивления внешней сети от 0 до xq (см. рис. 8.2).

______________

* Строго говоря, внутри зоны II можно выделить еще одну область, которую определяют иногда как область репульсионно-синхронного самовозбуждения. На границе этой области комплексные корни обращаются в два действительных кратных корня. Такое разделение зоны асинхронного самовозбуждения II на две области может способствовать уточнению характера процесса, но не имеет практического значения вследствие того, что репульсионно-синхронное самовозбуждение ни по визуальному наблюдению по приборам, ни по виду осциллограмм почти нельзя отличить от асинхронного. Кроме того, процесс самовозбуждения во всей зоне II не может быть устранен существующими в настоящее время АРВ синхронных машин. Способы выделения области репульсионно-синхронного самовозбуждения изложены в [Л.22].

8.2.7. Построение областей самовозбуждения II и III можно проводить, используя метод D-разбиения или пользуясь критерием Раусса.

8.2.8. При проектировании и в эксплуатационных расчетах границу асинхронного самовозбуждения допустимо определять приближенно только по зоне II. Для реально существующих постоянных времени обмотки возбуждения ≥ 4 с, можно принять, что зона асинхронного самовозбуждения II также ограничивается половиной окружности, радиус которой равен (xq - ) / 2. Центр окружности расположен на оси xc на расстоянии (xq + ) / 2 от начала координат. Максимальное значение активного сопротивления зоны II в этом случае равно

.                                                            (8.7)

Приближенной зоне асинхронного самовозбуждения II при незначительном сопротивлении r соответствует неравенство < xc < xq (см. пример 1 в приложении 14).

8.2.9. При малых значениях постоянной времени обмотки возбуждения машины ( ≤ 1 с), области асинхронного самовозбуждения II и III искажаются и должны находиться по критерию (8.4).

Наличие демпферных обмоток в продольной и поперечной осях ротора не влияет на границу зоны синхронного самовозбуждения, мало изменяет границы зоны II, но существенно расширяет зону III, наличие которой следует учитывать особенно в схемах с продольной емкостной компенсацией.

8.2.10. При малых значениях так же, как и при специальной конструкции демпферных обмоток с сильно увеличенными постоянными времени, определение зоны асинхронного самовозбуждения II необходимо проводить, используя критерий Гурвица (8.4). В этом случае в характеристическом уравнении (8.1) n = 7. Для расчетов на ЦВМ наиболее целесообразно использование критерия Раусса [Л.22, 31].

8.2.11. Приближенно зона самовозбуждения III определяется частотным методом [Л.22]. При скольжении порядка 20% и выше частотные характеристики машины с демпферными обмотками в обеих осях практически совпадают. В этих условиях синхронная машина может быть заменена асинхронной, частотная характеристика которой соответствует средней частотной характеристике реальной машины в осях d и q. Последние могут быть известны на основе экспериментальных данных или рассчитаны по выражениям xd(р) и xq(р) [Л.22, 31].

По частотному методу сопротивление машины представляют в виде

,                     (8.8)

где ω - частота свободных колебаний в роторе. При этом динамическая система, содержащая синхронную машину, преобразуется к статической схеме (рис. 8.3).

Граница области самовозбуждения III определяется условиями резонанса в рассматриваемой схеме и находится согласно выражениям

                                                    (8.9)

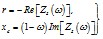
где 1-ω - частота свободных колебаний в схеме рис. 8.3.

При выполнении расчетов этим методом значения ω следует задавать от 0 до 1, определять Zг(ω), а затем по (8.9) вычислять r и xc. Расчет повторяется до получения всей границы зоны самовозбуждения III. После построения областей II и III их границы соединяются плавной кривой. Параметры внешней сети находят по аналогии с примером, рассмотренным выше.

Пример подобного рода расчетов имеется в [Л.24]. Другой способ нахождения зоны асинхронного самовозбуждения изложен в [Л.25].

8.2.12. Турбогенераторы, как магнитосимметричные машины, не имеют зоны синхронного самовозбуждения I. Полная зона асинхронного самовозбуждения (II и III) турбогенератора расположена в пределах

0 < xc < xd,                                                             (8.10)

При достаточно больших постоянных времени обмотки возбуждения турбогенераторов зона асинхронного самовозбуждения II в координатных осях r и хс приближенно описывается полуокружностью, центр которой расположен на оси ординат на расстоянии (xd + ) / 2 от начала координат, а радиус равен (хd - ) / 2.

Таким образом, границе зоны II, определенной в соответствии с принятыми допущениями, отвечают неравенства

                                                    (8.11)

8.2.13. Следует учитывать, что зона III асинхронного самовозбуждения турбогенераторов из-за их способности развивать достаточно большой асинхронный момент как при малых, так и больших скольжениях, значительно шире, чем у гидрогенераторов. Зону, асинхронного самовозбуждения III турбогенераторов, где xc < , целесообразно определять частотным методом [Л.24]. Обе зоны (II, III) самовозбуждения турбогенератора показаны на рис. 8.4.

Рис. 8.3. Схема замещения для расчета частотным методом зоны самовозбуждения III

8.2.14. Выявление условий самовозбуждения асинхронных машин изложено в [Л.22]. Примеры, связанные с выявлением условий самовозбуждения турбогенераторов и асинхронных машин приведены в [Л.24].

8.2.15. Исследование возможности устранения самовозбуждения синхронных машин с помощью автоматического регулирования возбуждения следует проводить, рассматривая систему уравнений, которая содержит уравнения переходного процесса в машине, уравнения переходного процесса в возбудителе и регуляторе в соответствии с видом регулирования возбуждения [Л.22, 26, 31]. Получающееся при этом характеристическое уравнение известными методами исследуется на устойчивость.

Как правило, АРВ пропорционального типа предотвращает развитие синхронного самовозбуждения. Пример определения коэффициентов усиления АРВ для устранения синхронного самовозбуждения приведен в [Л.24]. Существующими в практике эксплуатации современных энергосистем АРВ невозможно устранить развитие асинхронного самовозбуждения [Л.27].

Рис. 8.4. Зоны самовозбуждения турбогенератора:

-- при синхронной частоте;

------ при ω = 0,95

8.2.16. Учет распределенности параметров ВЛ при анализе самовозбуждения необходим при их длинах, равных 1200 км и более. При этом расширяется зона III асинхронного самовозбуждения. Поэтому эту зону для длин ВЛ более 1200 км рассчитывают с учетом распределенности параметров вдоль линии. При этом используют частотные характеристики машин xd (ω), xq (ω), rq (ω) и соотношения

zc ctg (1 - ω) λ = хвх = (1 - ω) х (ω),                                     (8.12)

r = - (1 - ω) r (ω),                                                        (8.13)

где jхвх - входное сопротивление холостой ВЛ без потерь*;

- волновое сопротивление ВЛ без потерь;

- волновая длина ВЛ без потерь, рад.;

; .

_________________

* Отказ от учета активных потерь в линии практически не изменяет границы зоны III.

Уравнение (8.12) определяет резонансную частоту ω. Это уравнение решается графически, для чего строятся зависимости (1 - ω) х (ω) и zc ctg (1-ω) λ = хвх от частоты свободных колебаний ω для разных заданных длин ВЛ. Точка пересечения этих кривых дает резонансную частоту для каждой из принятых длин линии l(λ), зная которую, из уравнения (8.13) определяют соответствующее граничное значение r. Расчеты повторяют при вариации длины ВЛ до получения границы зоны самовозбуждения.

Для выявления достаточных условий развития самовозбуждения вычисляют координаты точки, характеризующей конкретную внешнюю сеть, используя равенства

r = rвл + rген + rтр,

x = zc ctg (1-ω) λ + хтр,

где ω - резонансная частота, полученная из предшествующих расчетов;

rген - активное сопротивление генератора на частоте ω;

rтр, хтр - активное и реактивное сопротивления трансформатора.

Для определения активного сопротивления линии rвл используют соотношение

где

; θ < 0; φ = π + θ;

;

.

Если известны частотные характеристики ВЛ, то необходимость расчета rвл отпадает.

Возможны и другие методы учета распределенности параметров ВЛ, см. например, [Л.27, 28].

8.2.17. Самовозбуждение в условиях несимметрии параметров схемы и режима энергосистемы менее вероятно, чем при сохранении симметрии. Поэтому проверку энергосистемы на возможность появления самовозбуждения при несимметрии не проводят, если нет опасности самовозбуждения в условиях симметричности. Если же возникает необходимость такой проверки, то исходят из комплексных схем замещения энергосистемы [Л.29].

8.2.18. Если возникает необходимость в проверке отсутствия самовозбуждения при неноминальной частоте , то с достаточной степенью точности зоны самовозбуждения I и II могут быть найдены по уравнению

.                                (8.14)

_______________

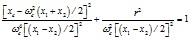
* При подъеме напряжения всей линии электропередачи или ее участков с нуля частота может быть ниже синхронной; при отказах, приводящих к разрыву передачи, возможно повышение частоты до 1,2-1,25 отн. ед. [Л.30].

В последнем уравнении при определении зоны I полагают x1 = xd, x2 = xq; для зоны II x1 = xq, x2 = xq. Каждая из зон I, II (см. рис. 8.2) ограничивается в плоскости r и xс полуэллипсом, координаты центров которых равны соответственно:

и . Зона III определяется частотным методом, описанным выше.

При частоте, отличной от синхронной, самовозбуждение принципиально возможно, если емкостное сопротивление внешней сети меньше (см. рис. 8.4, штриховые линии).

8.2.19. Номинальная мощность генераторов Sном, при включении которых на линию электропередачи длиной l самовозбуждение невозможно, рассчитывается по выражению [Л.30]

Sном / Sс = Sном* > xd ω tg (ωλ),                                              (8.15)

где xd = xdг + хтр - сопротивление генератора и трансформатора (отн. ед.), отнесенное к номинальной мощности генератора;

- натуральная мощность линии электропередачи.

Смотри также пример 2 в приложении 14.

8.2.20. Приближенная оценка возможности возникновения самовозбуждения при работе генераторов на холостую линию электропередачи выполняется следующим образом. Определяется входное сопротивление ВЛ

                                          (8.16, а)

для линий электропередачи длиной до 400 км и

                              (8.16, б)

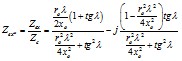
для линий длиной более 400 км.

Зависимости хвх* = f (l) для ВЛ напряжением 330-750 кВ и марок проводов от 2хАСО-300 до 4хACO-700 практически одинаковы (рис. 8.5).

Параметр генератора хd, хq, , а также трансформатора хт, rт определяются из равенства

,                                                            (8.17)

где х - взятое по каталожным данным соответствующее сопротивление генератора или трансформатора, отн.ед.

Рис. 8.5. Зависимость реактивной составляющей входного сопротивления холостой линии электропередачи 330-750 кВ от ее длины

Рис. 8.6. Определение зон самовозбуждения синхронной машины, работающей через сложную связь на мощную энергосистему:

а - общий вид схемы; б - расчетная схема замещения; в - зоны самовозбуждения I и II

В соответствии с критериями (8.2) на границе областей самовозбуждения имеют место следующие равенства

                                                   (8.18)

(при этом для гидрогенераторов не разделяются зоны I и II).

Зная значения параметров генераторов и трансформаторов, а следовательно хвх1* и хвх2* по уравнениям (8.16) или по рис. 8.5, находят предельные длины линий l1 и l2, причем l2 > l1, при включении на которые генератор может самовозбуждаться, см. пример 3 в приложении 14.

8.2.21. Для определения зон I и II самовозбуждения синхронной машины, работающей через сложную связь на мощную энергосистему (рис. 8.6), используют выражения, по которым приближенно можно найти границы зон самовозбуждения. Границе зоны I синхронного самовозбуждения для схемы, показанной на рис. 8.6, отвечает уравнение

(xd + Δx - xc) (xq + Δx - xc) + (r + Δr)2 = 0,                                  (8.19)

а границе зоны II асинхронного самовозбуждения соответствует уравнение

(x'd + Δx - xc) (xq + Δx - xc) + (r + Δr)2 = 0,                                  (8.20)

Значения Δx и Δr зависят от схемы внешней сети. В простейшем случае, показанном на рис. 8.6, б, они определяются параллельным сложением сопротивлений энергосистемы (jх2) и шунта нагрузки (rн + jxн). В общем случае значения Δx и Δr определяются по формулам, приведенным [Л.22, 31]. Граница зоны III асинхронного самовозбуждения находится частотным методом.

Зоны самовозбуждения при этом представляют собою части окружностей (см. рис. 8.6), центры которых находятся соответственно на расстоянии (xd + xq) / 2 + Δx и (x'd + xq) / 2 + Δx от оси ординат. Для сложной внешней сети емкостное сопротивление хс, при котором возможно самовозбуждение, увеличивается на значение Δх, а активное сопротивление, ограничивающее зоны I и II самовозбуждения, уменьшается на значение Δr. Примеры имеются в [Л.24]. Возможны и другие способы учета внешней сети [Л.28].

8.2.22. Методику определения условий самовозбуждения синхронных машин в сложных энергосистемах см. [Л.22, 31, 32].

8.3. Самораскачивание в энергосистемах

8.3.1. Самораскачивание, как особый вид нарушения статической устойчивости, исследуется на основе уравнении Парка-Горева, с учетом уравнения относительного движения ротора машины и активного сопротивления всех элементов энергосистемы [Л.33, 34].

8.3.2. Построение области самораскачивания выполняется аналогично показанному в [Л.3]. Для схемы, показанной на рис. 8.1, и при отказе от учета переходных процессов в статоре условия возникновения самораскачивания при этом определяются неравенствами

,                                                    (8.21)

,                                           (8.22)

где

; ;

;

.

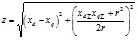
Эти условия определяют область самораскачивания с запасом.

8.3.3. Наличие продольной емкостной компенсации увеличивает область самораскачивания. При высокой степени продольной компенсации ВЛ верхнюю границу самораскачивания (8.21) следует уточнять по выражению

,

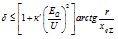
где

;

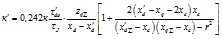
хс - сопротивление УПК.

Значение к принимается в соответствии с рис. 8.7.

8.3.4. О влиянии постоянной времени поперечного демпферного контура на условия самораскачивания см. в [Л.24]. Методика анализа возможности самораскачивания регулируемой синхронной машины при различных видах АРВ описана в [Л.22, 31]. Автоматические регуляторы возбуждения синхронных машин пропорционального и сильного действия устраняют самораскачивание при соответствующей их настройке.

Рис. 8.7. Зависимость поправочного коэффициента к от параметра r / xqΣ

при τJ = 6,25 с, = 5,5 с, EQ / U = 1, = 0,213

Глава 9. ПРИМЕНЕНИЕ ЦВМ ДНЯ АНАЛИЗА УСТОЙЧИВОСТИ

9.1. Общие указания

9.1.1. Электронные ЦВМ следует применять при анализе статической, динамической и результирующей устойчивости энергосистем, так как они дают возможность:

- повысить точность расчетов устойчивости энергосистем;

- приблизить расчеты к реальным условиям работы энергосистем, благодаря значительно большему соответствию действительных и расчетных схем энергосистемы (так как можно отказаться от упрощений значительной части основной схемы энергосистемы, а эквивалентирование остальных частей схемы производить с меньшей погрешностью), а также благодаря более полному учету различных автоматических устройств и эксплуатационных ограничений. При этом рассчитанные запасы устойчивости энергосистемы могут быть увязаны с реальными возможностями утяжеления режимов энергосистемы;

- ускорить выполнение расчетов (причем технические средства, внедряемые в энергетических организациях, дадут возможность при необходимости выполнять расчеты устойчивости также в процессе оперативного управления энергосистемами);

- выполнять расчеты большого количества вариантов, что дает возможность приблизиться к оптимальным решениям;

- использовать при анализе устойчивости энергосистем вероятностные методы.

Соответствующе алгоритмы и программы расчетов рекомендуется применять для анализа устойчивости с учетом влияния случайных погрешностей исходной информации на результаты расчетов устойчивости, на целесообразность уточнения (и усложнения) методов расчета, на сравнение эффективности способов повышения устойчивости, на сопоставление результатов расчета устойчивости с результатами натурных испытаний или экспериментов на динамических моделях энергосистем. При оценке запасов устойчивости может быть учтена случайная погрешность реализации рассчитанных режимов. Вероятностные методы могут быть применены для расчетов устойчивости межсистемных связей, для анализа некоторых вопросов ликвидации асинхронных режимов и др.

9.1.2. В специализированное математическое обеспечение (СМО) ЦВМ рекомендуется включать программы расчета устойчивости энергосистем, имеющие как более точные алгоритмы решения задачи (эти программы можно условно назвать эталонными), так и упрощенные алгоритмы (эти программы можно назвать серийными или стандартными). При выборе программы для расчетов следует учитывать, что эталонные программы требуют для расчета больше машинного времени, более обширную исходную информацию, и, следовательно, больше времени и труда на ее подготовку, а также больше времени на анализ результатов расчета. Необходимость применения таких программ обусловлена тем, что количественная оценка погрешностей применения упрощенных алгоритмов возможны в большинстве случаев только путем сравнительных конкретных расчетов по соответствующим эталонной и серийной программам. Такие сравнительные расчеты рекомендуется производить для типовых задач, выбранных в соответствии с имеющимся опытом проектирования, развития и эксплуатации энергосистем. В тех случаях, когда конкретные условия существенно отличаются от рассмотренных ранее типовых задач, следует снова произвести сравнительные расчеты по эталонной и серийным программам, имеющимся в СМО.

Эталонные программы могут быть использованы также самостоятельно для решения ответственных задач и для экспериментальных расчетов при исследовании допустимости упрощения эталонного алгоритма (задавая в исходной информации, например, различные значения параметров, влияние которых исследуется). Для полноты оценки допустимости применения серийной программы необходимо, чтобы в эталонной программе была предусмотрена возможность случайной вариации исходной информации для учета (например, по методу статистических испытаний) влияния неизбежной случайной погрешности исходных данных. Целесообразно также создание "библиотеки" примерных расчетов, выполненных по эталонным и серийным программам.

Использование эталонных программ или ранее выполненных по ним расчетов особенно важно при исследовательских расчетах, а также для предварительной оценки допустимости упрощений в серийных программах, обеспечивающих необходимое ускорение эксплуатационно-оперативных расчетов.

9.1.3. Поскольку результаты расчета устойчивости энергосистем (в особенности - сложных) зависят от достоверности задания и точности расчета исходных установившихся режимов энергосистемы и от неизбежного упрощения (эквивалентирования) расчетных схем, необходимо применять в комплексе с программами расчета устойчивости достаточно высококачественные программы предварительного упрощения действительной схемы энергосистемы и расчета ее установившегося режима, а также дальнейшего упрощения схемы для расчета устойчивости.

9.1.4. Для повышения эффективности применения ЦВМ при анализе устойчивости энергосистем следует совершенствовать ввод и вывод информации, в особенности автоматический контроль правильности вводимой и долговременно хранящейся во внешней памяти ЦВМ информации, возможность "диалога" с ЦВМ, печать схем сети и графиков с автоматическим нанесением результатов расчета, обозначений и пояснений, ввод для оперативных расчетов части информации через телемеханические каналы, использование телетайпной связи и т.д.

Поскольку для ЦВМ высокого класса предусматривается возможность параллельного решения нескольких задач, прерывание и возобновление вычислительного процесса, использование экранов электронно-лучевых трубок для оперативной информации о ходе вычислительного процесса (дисплей) и т.п., целесообразно обеспечивать хранение модели энергосистемы в долговременной памяти ЦВМ и рациональную организацию расчетов с помощью операционной системы (специализированной или общего назначения)*.

В составе СМО должны быть разработаны программы формирования и использования расчетно-базовых и расчетно-оперативных моделей энергосистемы.

Основные методы расчетов устойчивости и вопросы применения ЦВМ рассматриваются в [Л.35-74].

_________________

* Для ориентировки в этом направлении в приложении 15 в качестве примера кратко описана реализованная по заданию ЦПУ ЕЭС СССР система комплексного моделирования энергосистемы в памяти ЦВМ с программно-диспетчерским управлением обработкой информации и расчетами.

9.2. Расчет установившихся режимов при анализе устойчивости энергосистем

9.2.1. Если расчеты установившихся режимов являются самостоятельной задачей, то структура энергосистемы, средства регулирования напряжения, эксплуатационные ограничения и т.п. могут учитываться значительно более подробно, чем при расчетах устойчивости. Желательно, чтобы упрощение схем замещения энергосистемы для расчетов устойчивости производилось на основе предварительно рассчитанных нескольких (наиболее характерных при заданной постановке задачи) исходных установившихся режимов при максимальном объеме сети и полном учете ограничений, допускаемых соответствующей программой для ЦВМ.

При упрощении расчетных схем для анализа переходных процессов следует учитывать, что на результаты расчета могут оказать влияние и те факторы, которые не имеют значения, если рассчитываются только установившиеся режимы. В частности, должно учитываться возможное влияние относительного движения машин.

9.2.2. После произведенного тем или иным способом упрощения полной схемы энергосистемы исходный (для последующих расчетов устойчивости) установившийся режим должен быть рассчитан непосредственно для упрощенной расчетной схемы.

9.2.3. Эталонные программы для расчета на ЦВМ исходных установившихся режимов энергосистем должны обеспечивать возможность выполнения расчета как в устойчивой, так и в неустойчивой области режима энергосистемы. Серийные программы расчета исходных установившихся режимов могут обеспечивать возможность расчета лишь в устойчивой области работы энергосистемы (по пределу статической устойчивости), если это предусмотрено алгоритмом программы и при апробации программы проверено, что она обеспечивает возможность расчета режимов, достаточно близких к пределу устойчивости энергосистемы.

9.2.4. Расчеты установившихся режимов при номинальной частоте должны проводиться с учетом статических характеристик нагрузок по напряжению. В случаях, если по заданию устойчивость анализируется для установившихся режимов с частотой, существенно отличающейся от номинальной, например, при анализе реальных эксплуатационных или аварийных ситуаций, исходные данные для расчета такого режима должны учитывать зависимость параметров схемы от частоты.

9.3. Расчет предела статической устойчивости сложной энергосистемы

9.3.1. Статическая устойчивость энергосистемы по отношению к любым малым возмущениям (по виду и точке приложения) соответствует определению "устойчивости в малом" общей теории устойчивости Ляпунова и должна анализироваться при помощи ЦВМ по обоснованному Ляпуновым методу первого приближения [Л.1, 35-37].

В соответствии с этим для энергосистемы при определенных предпосылках определяются линеаризованные в точке исходного невозмущенного режима дифференциальные уравнения возмущенного (по Ляпунову) движения (предполагается в неявном виде возмущение начальных условий решения уравнений). Необходимым и достаточным критерием устойчивости энергосистемы является отрицательный знак действительных корней или действительной части комплексных корней характеристического определителя уравнений возмущенного движения.

9.3.2. Следует учитывать, что погрешность расчетов возрастает в основном из-за погрешности исходных данных при усложнении энергосистем и при более полном учете в модели энергосистемы автоматических регуляторов - в особенности при учете возможности самораскачивания в энергосистеме.

9.3.3. Расчеты статической устойчивости, выполняемые как при эксплуатации энергосистем, так и при проектировании их развития, дополнительно разделяются на два вида:

- выбор типа автоматических регуляторов и определение параметров их настройки;

- определение запасов устойчивости сложной энергосистемы.

Расчеты первого вида должны проводиться по полным критериям статической устойчивости (с учетом возможности самораскачивания). Подобные расчеты громоздки и трудоемки, поэтому при проведении их (даже при помощи ЦВМ) схему замещения энергосистемы приходится значительно упрощать, ограничиваясь варьированием типа и параметров АРВ на одной-трех электростанциях. При использовании результатов этих расчетов, в особенности при наладке автоматических регуляторов, параметры последних следует выбирать так, чтобы надежно исключить возможность самораскачивания.

Расчеты на ЦВМ целесообразно выполнять по программам определения границ областей устойчивости в плоскости двух параметров (большей частью - настроечных параметров АРВ). Желательна возможность задания серии расчетов с автоматическим изменением других параметров.

При выполнении расчетов второго вида допустимо полагать, что характеристики АРВ определены и заданы на основании типовых или конкретных расчетов или на основании специальных либо наладочных испытаний. Для расчетного определения запасов устойчивости необходимо стремиться к воспроизведению действительных условий работы энергосистемы как в отношении возможного утяжеления исходных режимов и учета различных ограничений, так и в отношении максимально возможного приближения расчетных схем замещения к реальным.

При этих расчетах очень сложно (и по изложенным выше соображениям практически нецелесообразно) использовать необходимые и достаточные условия отсутствия самораскачивания. Поэтому для подобных расчетов во многих случаях достаточно ограничиться анализом только апериодической (без учета самораскачивания) и "квазиапериодической" [Л.36, 46] устойчивости (с учетом возможности самораскачивания на низкой частоте). Допустимость такого упрощения может быть обоснована анализом устойчивости с учетом самораскачивания сравнительно простых схем замещения энергосистем или опытом эксплуатации данной энергосистемы (или энергосистем сходной структуры)*.

________________

* Опыт показывает, в частности, что при наладке AРB настроечные параметры устанавливаются с запасом по отношению к критическим (по условиям самораскачивания) значениям, выявленным наладочными испытаниями в контрольных режимах (запас необходим с учетом перспективы изменения структуры и режимов системы, а также с учетом возможной погрешности результатов расчетов, даже если они имели не типовой, а конкретный характер).

9.3.4. Проверка апериодической устойчивости выполняется по знаку свободного члена характеристического уравнения, проверка квазиапериодической устойчивости [Л.46] - кроме того и по знаку коэффициента предпоследнего члена. В обоих случаях проверяется также знак коэффициента a0. Эти критерии дают возможность учитывать как режимные параметры энергосистемы, так и влияние в явном виде АРВ.

Поскольку расчет для сложной энергосистемы представляет определенные трудности даже при использовании ЦВМ, то при проверке указанных критериев целесообразно для части синхронных машин энергосистемы отказаться от учета АРВ в явном виде, выполняя расчет при постоянстве фиктивных ЭДС этих синхронных машин, которые вводятся в схему замещения сопротивлением х в пределах между xd (отсутствие АРВ) и (АРВ пропорционального действия) или (АРВ сильного действия, 0 < а < 1); учет АРВ в неявном виде для части синхронных машин (электростанций) весьма упрощает проверку устойчивости.

Для оценки допустимости других приближенных критериев устойчивости и приближенного учета АРВ, а также для сравнительно ответственных эксплуатационных расчетов необходима программа расчета на ЦВМ, которая могла бы являться эталонной в рамках предпосылок для анализа статической устойчивости энергосистем.

9.3.5. Целесообразность усложнения или упрощения модели, реализуемой в эталонной программе, необходимо обосновывать с учетом влияния погрешности исходной информации на результаты расчетов* [Л.65-68].

_______________

* В сравнительно простых вариантах алгоритмов, позволяющих рассчитывать критерии апериодической и квазиапериодической устойчивости, учитывается регулирование возбуждения синхронных машин в зависимости от отклонения и от производных тока, напряжения и абсолютного угла и зависимость механического момента от частоты вращения при постоянном коэффициенте результирующего демпфирования [Л.45].

9.3.6. Для нахождения предела и определения запасов статической устойчивости используется метод последовательного изменения (утяжеления) исходного режима с проверкой для утяжеленного режима критерия устойчивости.

Возможны случаи, когда предельный режим обуславливается не устойчивостью системы, а осуществимостью установившегося режима при заданных ограничениях. Если расчеты выявили, что предельные по эксплуатационной осуществимости режимы являются устойчивыми или весьма близки к пределу устойчивости, можно в дальнейшем, для сходных по расчетным условиям вариантов или новых заданий не проверять критерий устойчивости, что соответственно упрощает и ускоряет решение задачи о предельных режимах.

9.3.7. Следует различать два вида ограничений, задаваемых (или рассчитываемых по некоторому алгоритму) при утяжелении исходных стационарных режимов энергосистемы:

- ограничения длительно допустимых эксплуатационных режимов (эксплуатационные ограничения). К ним относятся нормативные условия допустимой перегрузки по току или по тепловому режиму машин, трансформаторов и других элементов системы (формулируемые часто как ограничения располагаемой реактивной мощности), ограничения по перетокам в некоторых линиях электропередачи, по уровням напряжения в заданных точках сети, по допустимым отклонениям частоты и т.п.;

- ограничения режимов, которые возможны и допустимы лишь кратковременно, но устойчивость энергосистемы в которых еще может сохраняться, что должно быть проверено расчетом (технические ограничения). Ограничения в этих режимах определяются техническими характеристиками элементов энергосистемы (например, потолком возбуждения машин, форсировочной способностью автоматических регуляторов, уставкой автоматов безопасности турбин при повышенной частоте, уставкой частотной разгрузки при пониженной частоте и т.п.).

9.3.8. При расчетном утяжелении режимов энергосистемы возможен выход на эксплуатационные ограничения еще до предела статической устойчивости. В этом случае расчетом выявляются пределы осуществимости утяжеления в отношении длительно допустимых эксплуатационных режимов. Для оценки практической допустимости этих режимов (в отношении устойчивости) необходимо продолжить их расчетное утяжеление, заменив в расчете те эксплуатационные ограничения, которые не обеспечиваются сравнительно быстродействующий автоматическими устройствами, на технические ограничения. Это определит запас статической устойчивости энергосистемы при данном способе утяжеления исходного режима. Кроме того, определение нарушения эксплуатационных ограничений, например при анализе возможных послеаварийных ситуаций, даст ориентировку для обеспечения автоматического или диспетчерски управляемого перевода энергосистемы в область длительно допустимых устойчивых режимов.

9.3.9. Расчетное утяжеление режима при плановых, и, в будущем, при оперативных расчетах в соответствии с заданиями, анализирующими реальные условия работы энергосистемы и варианты диспетчерского управления, рекомендуется осуществлять следующими основными способами:

- увеличением общей нагрузки (и генерации) энергосистемы в заданных узлах сети с возможностью различного шага утяжеления в этих узлах;

- перераспределением нагрузок между генерирующими узлами;

- снижением напряжения в заданных узлах сети (изменением фиксированного модуля напряжения или реактивной мощности в узлах).

Возможно также комбинирование указанных способов утяжеления.

9.3.10. При выполнении расчетов следует учитывать, что в большинстве имеющихся программ для ЦВМ второго поколения утяжеление стационарных режимов производится при допущении о неизменности частоты. Балансирующие активную мощность узлы сети рекомендуется совмещать с шинами электростанций, регулирующих частоту. Балансирование реактивной мощности наполняется всеми узлами, в которых задается фиксированные по модулю напряжения или статические характеристики нагрузки Qн (U).

Для использования программ, позволяющих рассчитывать утяжеление исходного режима с учетом изменений частоты, необходимо вводить дополнительную информацию: статические характеристики зависимости активной и реактивной мощности нагрузки и генерации от частоты. Должны изменяться также ограничения режима. ЦВМ третьего поколения позволяет выполнять такие расчеты утяжеления режима с необходимой полнотой.

9.3.11. Выявление при анализе устойчивости энергосистемы ее "слабых" звеньев, определяющих уровень устойчивости всей энергосистемы, достигается последовательным сравнением результатов расчета устойчивости для заданной схемы замещения и схем, в которых сомнительные звенья исключаются при помощи известных способов упрощения энергосистемы. Возможно также выполнение для этой цели расчетов переходных процессов в той же схеме замещения энергосистемы при конкретных малых возмущениях, выявляющее сравнительно большие отклонения режима или нарушение устойчивости слабых звеньев энергосистемы.

Если имеются опасения, что при упрощении исходной схемы энергосистемы были устранены слабые звенья (возможность выявления неустойчивости движения внутри группы машин, объединенных в одну эквивалентную машину), можно при необходимости повторить расчет, расчленив эквивалентную машину на две машины, или восстановив в схеме другие предположительно слабые звенья.

Для ЦВМ третьего поколения желательна разработка специальной подпрограммы "диагностики" типовых расчетов для выбора вариантов эквивалентирования больших схем и определения "слабых звеньев".

9.4. Расчеты динамической устойчивости и электромеханических переходных процессов

9.4.1. В соответствии с общей теорией устойчивости Ляпунова понятию динамической устойчивости энергосистемы должно было бы соответствовать определение "устойчивости в большом" энергосистемы, основанное на анализе нелинейных дифференциальных уравнений возмущенного (по Ляпунову) движения. В практике анализа режимов энергосистем понятию динамической устойчивости соответствует определение электромеханического переходного процесса для заданного ограниченного интервала времени при заданном конкретном возмущении [Л.3, 35].

При этом переходный процесс определяется путем численного интегрирования нелинейных уравнений динамики энергосистемы (с учетом автоматических регуляторов непрерывного действия и автоматических устройств дискретного действия). Применение ЦВМ дает возможность производить расчеты для достаточно сложных схем замещения (математических моделей) энергосистемы при достаточной длительности рассчитываемой части переходного процесса. Точность результатов расчета для заданной модели системы ограничивается, главным образом, точностью исходной информации (включая информацию об исходном установившемся режиме). Погрешность расчетов возрастает с увеличением в рассчитываемом переходном процессе числа колебательных циклов проверяемых координат (обычно, углов между ЭДС синхронных машин), в особенности, если расчет выявляет возникновение асинхронного хода в энергосистеме.

9.4.2. Относительно практической целесообразности анализа устойчивости энергосистема "в большом", по прямому методу Ляпунова (соответствующие программы разрабатываются) необходимо иметь в виду следующее:

- в разработанных программах до расчета по прямому методу Ляпунова все же применяется расчет переходного процесса (численным интегрированием). Лишь после того, как этот расчет охватит все заданные конкретные возмущения (например, двухфазное КЗ в начале заданной линии электропередачи, ликвидируемое каскадным отключением с двух сторон поврежденной цепи, автоматическое повторное включение поврежденной цепи и повторное ее отключение, срабатывание других устройств противоаварийной автоматики и т.п.), расчет переходного процесса может быть прекращен и зафиксированы начальные условия для дальнейшего расчета по прямому методу Ляпунова;

- расчет может определить лишь достаточные (но не необходимые) условия устойчивости при дальнейшем переходном процессе без дополнительных конкретных возмущений. Поэтому в большинстве случаев остается необходимым рассчитать также статическую устойчивость для самоустанавливающегося послеаварийного режима. Этот расчет следует проводить для математической модели, значительно более приближающейся к реальным условиям послеаварийного режима (обычно утяжеленного), чем модель, используемая в расчете по прямому методу Ляпунова. Это важно не только для проверки устойчивости послеаварийного режима энергосистемы, но и для оценки запаса статической устойчивости этого режима;

- если самоустанавливающийся послеаварийный режим может быть реализован лишь кратковременно, то необходимо рассчитать длительно допустимый (при возникших условиях) режим, в которой может быть переведена энергосистема.

В алгоритмах эталонных программ расчета динамической устойчивости, в зависимости от их назначения, желательно предусматривать (помимо того, что учитывается в серийных программах) хотя бы для нескольких синхронных машин учет полных уравнений Парка-Горева, учет влияния магнитного насыщения, уточненный учет автоматического регулирования возбуждения и скорости машин, уточненный учет действия устройств противоаварийной автоматики. Желательно также использование достаточно точного метода численного интегрирования (желательно с оценкой накопляющейся погрешности), учет волновых процессов в длинных линиях электропередачи, возможность учета случайных вариаций исходных данных и автоматической статистической обработки серии расчетов по методу статистических испытаний.

9.4.3. При проведении расчетов динамической устойчивости по серийным программам рекомендуется определять исходный доаварийный режим в соответствии с приведенными выше указаниями (п.9.2). В программах целесообразно предусматривать проверку сбалансированности введенного в расчет исходного режима (возможны как ошибки в задании исходных данных, так и ошибки при вводе информации в ЦВМ). Такая проверка может состоять в том, что по программе расчета динамической устойчивости рассчитываются сначала несколько интервалов времени при отсутствии заданного возмущения. Это позволяет убедиться в том, что результаты расчета этих интервалов совпадают с данными исходного доаварийного режима. В программе должна быть предусмотрена печать фактически введенных в ЦВМ исходных данных.

9.4.4. В программах следует предусматривать возможность учета уравнений асинхронных двигателей (см. гл. 6), а также статические характеристики нагрузки, как обобщенные (см. гл. 2), так и с конкретно задаваемыми коэффициентами описывающих их полиномов.

9.4.5. Рекомендуется при отсутствии других возможностей оценивать точность численного интегрирования путем уменьшения шага интегрирования. Такую оценку желательно производить в начале расчета и в той его части, когда контролируемые параметры переходного процесса изменяются с наибольшей скоростью (если в программе расчета на ЦВМ не предусмотрено автоматическое изменение шага интегрирования).

9.4.6. В зависимости от назначения расчетов целесообразно осуществлять печать и отображение на ЭЛТ графиков (для оперативной оценки хода и результатов расчетов) и печать таблиц в конце расчета (для более подробной и окончательной оценки результатов расчета).

9.4.7. Рекомендуется проводить серии расчетов при обоснованном выборе необходимых вариантов по исходному режиму, возмущению, параметрам устройств противоаварийной автоматики и др.

9.4.8. При расчете на ЦВМ длительных электромеханических переходных процессов, в особенности включающих в себя асинхронный ход и его ликвидацию (расчет результирующей устойчивости), рекомендуется следующее: использование для эквивалентных машин, частота вращения которых в переходном процессе может измениться наиболее значительно, уравнений Парка-Горева, уточненной математической модели АРС, учет асинхронных (и при необходимости синхронных) двигателей в тех узлах сети, в которых может быть значительное изменение напряжения, определение в ходе расчета режимных параметров, от которых зависит действие соответствующих релейных защит и устройств противоаварийной автоматики; применение сравнительно более точного метода численного интегрирования, желательно с оценкой накопляющейся погрешности.

9.4.9. Пои определении токов и напряжений в различных звеньях энергосистемы в заданные моменты времени электромеханического переходного процесса следует иметь в виду, что в несимметричных режимах (например, до отключения несимметричного КЗ во всех фазах или при неполнофазных режимах) по используемым в настоящее время программам расчета на ЦВМ определяются токи и напряжения прямой последовательности фаз. Для ЦВМ третьего поколения программы могут быть модифицированы для расчета токов и напряжений других последовательностей.

Определение эквивалентного шунта в схеме замещения энергосистемы при несимметричном КЗ может производиться по программе расчета схем замещения нулевой и обратной последовательности или по программе, в которой задается снижение напряжения прямой последовательности в точке КЗ (и мощность, потребляемая шунтом). Второй вариант программы целесообразен в случае отсутствия достоверных данных о параметрах схем нулевой и обратной последовательности.

Характеристику программ для расчетов динамической устойчивости энергосистем см. в приложении 16.

9.5. Применение метода статистических испытаний для анализа влияния случайных погрешностей исходной информации и реализации результатов расчета устойчивости на ЦВМ

9.5.1. Анализ устойчивости энергосистем должен проводиться с учетом случайных отклонений (погрешности) исходных данных, принятых для расчета, от фактических значений. Необходимо учитывать также, что при реализации результатов расчета неизбежны случайные отклонения фактических значений параметров режима энергосистемы от значений, фиксируемых с помощью измерительных устройств. Эти отклонения вызываются погрешностью измерений (погрешности измерительной и преобразовательной аппаратуры -трансформаторов тока и напряжения, каналов телепередачи и т.п.). Влияние этих случайных погрешностей в многочисленных звеньях энергосистемы должно определяться с учетом вероятности как взаимной компенсации, так и взаимного усиления, так как отклонения могут иметь разные знаки. Для решения этой задачи целесообразно применять метод статистических испытаний [Л.65-68] , который при использовании ЦВМ является практически выполнимым. В соответствии с этим методом на ЦВМ многократно повторяется расчет по детерминистически построенной основной подпрограмме анализа устойчивости, но для каждого расчета по дополнительным подпрограммам производится вариация случайными числами вводимых исходных данных. Эта вариация производится в пределах, заданных для каждого параметра или для групп параметров, при заданных законах распределения вероятности. Результаты многократно повторяемых детерминистических расчетов обрабатываются специальной подпрограммой по методам математической статистики, при этом выполняется минимально необходимое для представительности статистики количество повторяемых расчетов. Таким образом, осуществляется статистическое моделирование на ЦВМ необходимого числа "испытаний" при случайной вариации различных параметров*.

________________

* Случайные числа, необходимые при решении задачи, целесообразно вырабатывать с помощью специальных подпрограмм на ЦВМ.

Для различных ЦВМ имеется большая библиотека подпрограмм датчиков псевдослучайных чисел (ПДСЧ) с различными законами распределения (равномерный, нормальный, биномиальный и т.д.). В связи с многомерностью задач анализа устойчивости энергосистем и ограниченной поэтому возможностью проведения большого числа испытаний на ЦВМ, к ПДСЧ предъявляются повышенные требования. Кроме проверки их по стандартным тестам, желательно проверять с заданной доверительной вероятностью предельные отклонения статистических характеристик выборок из ПДСЧ по числу варьируемых исходных параметров, а также оценивать независимость этих выборок. [Л.67].

9.5.2. Диапазон отклонений значений, принимаемых для расчета, от возможных фактических параметров, а также законы распределения отклонений следует определять предварительным анализом статистических данных, если они имеются. При отсутствии статистики (во многих случаях имеется еще недостаточное количество данных) необходимо принимать во внимание особенности отклонений параметров различного типа. Погрешности измерений сложными измерительными устройствами подчиняются, как правило, нормальному закону. Параметры элементов энергосистем, используемые в расчетах устойчивости, большей частью не измеряются непосредственно, а вычисляются с помощью исходных величин, определяемых экспериментально. В этом случае диапазон отклонений и закон распределения отклонений параметров зависят от количества исходных величин, по которым они определяются, от вида функциональной связи между ними, от ошибок исходных величин. При полном отсутствии экспериментальных данных по каким-либо параметрам (прогнозируемая нагрузка, проектные длины линий) диапазон отклонений следует задавать ориентировочно на основании соображений о возможных отклонениях таких параметров. Распределение отклонений для подобных параметров можно принимать равномерным.

Следует учитывать, что степень влияния погрешностей исходных параметров на результат расчета устойчивости неодинакова.

Все исходные для расчета параметры можно разделить на "существенные" - изменение которых в заданных границах существенно сказывается на результаты расчета, и "несущественные" - изменение которых в меньшей (заданной) степени, по сравнению с первыми, влияет на результат. "Несущественные" параметры можно задавать в расчетах фиксированными. К точности определения "несущественных" параметров можно не предъявлять высоких требований.

9.5.3. Количество возможных комбинаций отклонений параметров может быть очень велико. Чтобы уменьшить число вариаций (имитирующих случайные отклонения) исходных параметров, а значит, и затраты машинного времени, следует определять минимально необходимое число испытаний (реализаций), при котором получаются достоверные результаты анализа с необходимой точностью.

9.5.4. Получаемая посредством многократных расчетов устойчивости энергосистемы совокупность случайных значений результата расчетов должна быть подвергнута статистической обработке, в результате которой может быть получен ее закон распределения (в графическом или аналитическом виде) и числовые характеристики с оценкой их относительной погрешности: среднее значение, дисперсия, коэффициент вариации, вероятность нарушения устойчивости и др. [Л.65-68].

При оценке влияния погрешности исходной информации в расчетах устойчивости необходимо задавать погрешность исходных данных, начиная с расчета доаварийного режима, поскольку его параметры оказывают существенное влияние на результаты анализа устойчивости.

9.5.5. Расчеты устойчивости энергосистем при учете погрешности исходной информации следует выполнять на ЦВМ с помощью комплексов программ, включающих основные серийные или эталонные программы расчета установившегося электрического режима, динамической или статической устойчивости, блоки вариации исходных данных и статистической обработки результатов счета. Основные программы модифицируются для сокращения объема печати при многократных расчетах и для осуществления связи с программой статистической вариации.

При вероятностной оценке влияния погрешности исходных данных нет необходимости получать в каждом расчете такую же полную информацию об устойчивости режима, как в детерминистическом расчете. Например, при анализе динамической устойчивости с учетом неточности исходных данных не нужно полностью выводить на печать все кривые изменения относительных углов роторов синхронных машин, а достаточно в поставленной задаче определить лишь, например максимальные или минимальные значения относительных углов; в расчетах статической устойчивости не нужно находить границы областей устойчивости, а лишь ее размеры. Полная информация о результатах расчета устойчивости при необходимости получается после оценки влияния погрешности исходных данных путем использования немодифицированной основной программы.

9.5.6. Сопоставление результатов расчетов между собой (например, при сравнении более точного и упрощенных методов), а также с данными опытов следует связывать оценками типа "разница находится (или не находится) в пределах точности исходных расчетных данных и точности измерения".

Эта оценка до последнего времени делалась весьма ориентировочно и большей частью основывалась лишь на инженерной интуиции. Метод статистических испытаний на ЦВМ дает возможность получить расчетно-аналитическое обоснование этой оценки при учете влияния неточности исходной информации на результаты расчета устойчивости энергосистем и неточности измерений при реализации результатов этих расчетов. При выборе метода анализа устойчивости энергосистем слезет также иметь в виду и чувствительность методов к вариации параметров расчета. Эта чувствительность может оказаться разной для различных методов и алгоритмов, несмотря на то, что они полностью эквивалентны при однозначном представлении исходных данных. Применение метода статистического моделирования на ЦВМ дает возможность исследовать чувствительность различных методов (алгоритмов) анализа устойчивости энергосистем в статистическом плане, без детального изучения внутренней структуры метода.

Указанные расчеты в основном должны иметь характер типовых, чтобы не было необходимости выполнять их в полном объеме для каждого конкретного случая.

Пример расчета динамической устойчивости на ЦВМ с учетом влияния случайной погрешности исходной информации приведен в приложении 17.

9.5.7. Обоснование нормативных показателей устойчивости энергосистем должно производиться с помощью статистико-вероятностных методов анализа, поскольку число, вид, место и длительность нарушения устойчивости в энергосистеме, а также погрешность реализации результатов расчетов являются случайными величинами. При определении нормативных показателей с помощью вероятностных характеристик, полученных в результате вероятностного анализа устойчивости, необходимо учитывать случайную погрешность исходных данных как в анализе устойчивости, так и в технико-экономических расчетах, в которые наряду с капиталовложениями и эксплуатационными расходами войдет и народнохозяйственный ущерб от перерывов электроснабжения.

Глава 10. ПРОВЕДЕНИЕ НАТУРНЫХ ИСПЫТАНИЙ И ИХ ИСПОЛЬЗОВАНИЕ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ ЭНЕРГОСИСТЕМ

10.1. Общие указания

10.1.1. Натурные испытания проводятся с целью уточнения областей устойчивости*, выбора настройки устройств регулирования и противоаварийной автоматики, оценки устойчивости нагрузки, изучения сложных переходных процессов, определения эффективности различных противоаварийных мероприятий, уточнения математического описания энергосистемы и определения параметров ее элементов [Л.75-77].

_______________

* Необходимость возможно точного определения устойчивости в условиях эксплуатации связана также с тем, что в ряде случаев для предотвращения ограничения потребителей или потери гидроресурсов в соответствии с нормативами [Л.7] допускается длительная работа линии электропередачи с запасом по статической устойчивости, уменьшенным до 5-10% (в зависимости от роли линии электропередачи в энергосистеме и последствий возможного нарушения устойчивости). Работа с такими малыми запасами устойчивости осуществима только при условии детального анализа условий работы линии электропередачи и проведения экспериментов, необходимых для выявления фактических пределов устойчивости.

10.1.2. Как правило, выбор оптимальной по условиям обеспечения устойчивости настройки автоматических устройств (сильного регулирования возбуждения, противоаварийной автоматики, устройств аварийной разгрузки линии электропередачи и т.д.) следует осуществлять с помощью специальных натурных испытаний.

10.1.3. Проведение натурных экспериментов представляет собой сложную задачу, связанную с большой подготовкой организационного характера, установкой необходимой регулирующей аппаратуры, средств измерения и регистрации параметров режима и созданием необходимых схем и режимов; во многих случаях опыты сопровождаются серьезным нарушением режима работы энергосистемы (объединения). Количество опытов поэтому следует жестко ограничивать. Для определения устойчивости при большом разнообразии эксплуатационных схем и режимов необходимо сочетать натурные испытания с расчетами или исследованиями на моделях. При этом натурные испытания следует использовать не только для непосредственных выводов из наблюдаемых процессов, но и для уточнения расчетной методики и выявления параметров, необходимых для моделирования энергосистемы, что позволяет получать достоверные результаты для других схем и режимов, в частности, для режимов, которые не могут быть воспроизведены в натуре.

10.1.4. Испытания не должны исключать расчетов по определению пределов устойчивости, а должны использоваться для уточнения этих пределов. Как правило, испытаниям должно предшествовать расчетное определение устойчивости.

10.2. Экспериментальное определение пределов статической устойчивости

10.2.1. Испытания статической устойчивости в условиях эксплуатации чаще всего проводятся с целью определения предельных значений мощностей, передаваемых по линиям электропередачи. Помимо этого, такие испытания проводятся для проверки устойчивости заданного режима, определения уровней напряжения в различных точках энергосистемы, выбора коэффициентов настройки регуляторов возбуждения сильного действия и т.д. Экспериментальное определение предельной по статической устойчивости загрузки линий электропередачи (Рпред) следует проводить в особенности в относительно сложных энергосистемах, когда расчет предела по статической устойчивости наталкивается на серьезные трудности, так как требуется учет большого числа факторов.

10.2.2. Следует также уточнять значения Рпред для межсистемных слабых связей, предельная пропускная способность которых соизмерима с величиной нерегулярных колебаний мощности. Отсутствие данных по действительному значению Рпред при этих условиях может привести к работе с неоправданно большим запасом, или напротив, к частым нарушениям устойчивости вследствие недостаточного запаса по статической устойчивости. Кроме того значение Рпред необходимо для правильного выбора уставок реле и устройств противоаварийной автоматики, предназначенной для предотвращения нарушения устойчивости.

10.2.3. Методика проведения испытаний. Экспериментальное определение Рпред может быть выполнено следующими двумя способами:

- путем постепенного увеличения передачи мощности по линии электропередачи до предела по статической устойчивости;

- путем создания качаний по испытуемой линии электропередачи, при которых передаваемая мощность проходит максимальные значения.

При втором способе линия электропередачи, для которой требуется определить Рпред, включается несинхронно при незначительном скольжении между частями энергосистемы (порядка долей процента), но при угле δ в пределах 120-150°. Синхронизация в этом случае, как правило, происходит без асинхронного хода. Однако в результате включения с большим углом в энергосистеме возникают синхронные качания, при которых угол передачи проходит значения ±90°. Это дает возможность по записи значения активной трехфазной мощности определить Рпред при передаче мощности как в одном, так и в противоположном направлении.

10.2.4. Испытания должны проводиться при полном рабочем напряжении и включенных в работу устройствах АРВ. В течение опыта персонал не вмешивается в работу систем автоматического регулирования мощности и напряжения.

10.2.5. Первый способ следует использовать, если необходимо выявить возможность колебательного нарушения устойчивости. Второй способ следует использовать при определении предела статической устойчивости по слабой связи. В остальных случаях выбор способа следует производить с учетом табл. 10.1.

Таблица 10.1

10.2.6. Для устранения раскачивания и предотвращения нарушения устойчивости параллельной работы при использовании первого способа рекомендуется:

- быстрое уменьшение мощности, передаваемой по линии электропередачи (например, быстрая загрузка генераторов в приемной части энергосистемы) или разгрузка (отключение) некоторых генераторов в передающей части энергосистемы;

- включение второй параллельной линии электропередачи;

- форсировка возбуждения генераторов передающей электростанции.

Если нарушение устойчивости имеет апериодический характер, сопровождаемый самопроизвольным ростом угла δ, то предотвратить возможность нарушения устойчивости затруднительно.

10.2.7. Следует иметь в виду, что если устойчивость будет нарушена при первом способе определения Рпред, то есть при передаче по линии электропередачи в исходном режиме максимальной мощности, то в этом случае в приемной энергосистеме (если ее мощность соизмерима с Рпред) будет глубокое понижение частоты и возможно отключение потребителей от АЧР, что нежелательно.

10.2.8. Порядок подготовки и проведения испытаний. Объем подготовительных работ в значительной мере определяется выбранным способом испытаний. При первом способе испытаний основное внимание должно быть уделено организационной стороне проведения опыта, так как при нечеткой организации опыта возможно нарушение устойчивости с соответствующими для энергосистемы последствиями. При втором способе основная подготовительная работа связана с определением допустимости применения несинхронного включения линии и установления величины скольжения, при котором будет иметь место синхронизация без асинхронного хода, т.е. подготовка обязательно связана с проведением предварительных аналитических расчетов.

10.2.9. Подведение к пределу статической устойчивости при использовании первого способа осуществляется увеличением передаваемой мощности при соответствующем уменьшении нагрузки электростанциями приемной энергосистемы и поддержании нормальной или несколько повышенной частоты (до 50,2-50,4 Гц); при этом вращающийся резерв мощности в приемной энергосистеме увеличивается и при приближении к ожидаемому пределу должен быть доведен до значения, при котором прекращение передачи мощности и наброс на приемную энергосистему части потерь в линии электропередачи при асинхронном режиме не приведут к опасным нарушениям работы потребителей и снижению частоты до значения, близкого к уставке АЧР.

10.2.10. Увеличение передаваемой мощности должно проводиться плавно и небольшими ступенями, в особенности в области, близкой к пределу по устойчивости, при непрерывном осциллографировании процесса, что дает возможность более точно определить предел устойчивости.

10.2.11. Для предотвращения ложной работы устройств релейной защиты и автоматики, в особенности дистанционной защиты третьей ступени, реагирующей на перегрузку линии электропередачи, необходимо принятие соответствующих мер (перевод на сигнал, загрубление защиты и т.п.).

10.2.12. Если асинхронный режим в энергосистеме нежелателен или недопустим, то при первых признаках, указывающих на возможность нарушения устойчивости (резкое увеличение реактивной мощности и тока линии электропередачи; возникновение синхронных колебаний тока, напряжения и мощности с нарастающей амплитудой) срочно принимаются меры по предотвращению нарушения синхронизма путем включения параллельной или обходной линии электропередачи, отключения части генераторной мощности в передающей части энергосистемы или экстренной загрузки генераторов в приемной части энергосистемы и т.д.

10.2.13. Проверку возможности определения Рпред по второму способу следует начинать с расчета токов несинхронного включения и выяснения допустимости его применения с точки зрения воздействия токов и моментов, возникающих при этом в генераторах и трансформаторах энергосистемы. Так как в опыте включение может произойти с произвольным углом, расчет должен производиться для наиболее неблагоприятного угла включения.

Проверка допустимости применения несинхронного включения с точки зрения воздействия токов и моментов производится по критериям и методике [Л.78, 79]. По [Л.78] проверке подлежат все элементы энергосистемы, по которым будут протекать наибольшие токи при несинхронном включении.

Учитывая, что несинхронное включение осуществляется при установившемся режиме и при нормальной частоте, в качестве критериев допустимости применения несинхронного включения могут быть использованы критерии, вычисленные при условии (см. гл. 5).

10.2.14. Если асинхронный режим недопустим, то должны быть приняты меры, обеспечивающие отключение линии электропередачи при первых признаках асинхронного хода (настройкой существующих защит или устройств противоаварийной автоматики или установкой дополнительных автоматических устройств).

10.2.15. В случае допустимости асинхронного хода, как правило, целесообразно совмещение испытаний статической устойчивости с испытанием кратковременного асинхронного хода и проверкой успешности ресинхронизации после автоматической разгрузки линии электропередачи.

10.2.16. Испытания в энергосистеме, независимо от принятого способа, проводятся по программе, в которой должны быть отражены следующие вопросы:

а) цель испытаний;

б) подготовительные работы по схеме, оснащению объектов необходимой для испытаний аппаратурой, выявлению параметров и настройке регулирующих устройств и т.д.;

в) режим энергосистемы в период испытаний;

г) объем испытаний с краткой характеристикой и порядком проведения опытов;

д) перечень мероприятий по релейной защите и автоматике, необходимых для проведения опытов, а также для предотвращения ложного действия устройств защиты и автоматики при асинхронном режиме, в том числе и при несинхронном включении;

е) указания по осциллографированию и записи показаний приборов на основных объектах с разработанными бланками записи всех необходимых величин (ток, напряжение, активная и реактивная мощности, частота, напряжение биений на контактах отключенного выключателя и т.п.);

ж) указания оперативному персоналу по проведению ресинхронизации при возникновении асинхронного хода в энергосистеме или об осуществлении деления, если невозможно обеспечить ресинхронизацию или недопустим даже кратковременный асинхронный ход;

з) распределение обязанностей между персоналом, участвующим в проведении испытаний, руководство испытаниями и ответственные лица.

10.2.17. Для подготовки указаний персоналу на случай возникновения длительного асинхронного хода при предварительных расчетах должны быть определены точки деления, наиболее целесообразные по балансам мощностей в энергосистеме. Если при возникновении асинхронного хода, несмотря на принятые меры, не удается своевременно осуществить ресинхронизацию, то по команде руководителя испытаний производится деление энергосистемы в указанных точках.

10.3. Экспериментальное определение динамической устойчивости

10.3.1. Целью таких испытаний является уточнение пределов динамической устойчивости энергосистемы при изменении эксплуатационных схем и режимов, а именно:

- определение максимально допустимого времени КЗ по условиям сохранения устойчивости для заданного значения передаваемой мощности по линии электропередачи;

- определение максимально допустимой мощности, передаваемой по линии электропередачи, при заданной длительности КЗ по условиям сохранения устойчивости;

- проверка эффективности действия и настройки устройств противоаварийной автоматики, предназначенной для предотвращения нарушения устойчивости при различных аварийных возмущениях в энергосистеме (например, проверка работы устройств аварийной разгрузки линии электропередачи при КЗ и отключении одной из параллельных линий) и т.п.

10.3.2. В условиях эксперимента не обязательно утяжелять условия опыта с доведением до нарушения устойчивости. Достаточно дать значительное возмущение, выбранное на основании предварительных расчетов так, чтобы получить динамический процесс, близкий к предельному по устойчивости. После проведения эксперимента необходимо выполнить расчеты для условий опыта и добиться хорошего совпадения результатов, уточнив по данным эксперимента влияние автоматического регулирования и других факторов.

10.3.3. Конкретно расчетный вид возмущения определяется в соответствии с нормативами [Л.7] или исходя из специфических местных условий.

10.3.4. Основная подготовительная работа связана с выбором схемы и режима энергосистемы на период испытаний. Испытания проводятся в соответствии с рабочей программой, составленной по тому же образцу, как и при испытаниях статической устойчивости (п. 10.2). В опытах определения динамической устойчивости очень важно обеспечить заданную длительность КЗ и селективное его отключение. Само КЗ осуществляется, как правило, включением на закоротку свободного выключателя или освобождается одна система шин, на которой устанавливается закоротка, и включение производится междушинным выключателем. На защите выключателя предварительно устанавливается требуемая уставка и производится проверка работы привода и времени действия защиты и выключателя. Независимо от данной проверки предусматривается резервирование отключения КЗ (на случай отказа основного выключателя) другими выключателями, уставка защит которых отстраивается по времени на одну ступень (или при необходимости устанавливается та же выдержка времени).

10.3.5. При проведении опытов определения динамической устойчивости в остальном следует руководствоваться указаниями, приведенными выше, для определения статической устойчивости.

10.4. Экспериментальное определение результирующей устойчивости

10.4.1. Аналитические расчеты условий ресинхронизации после нарушения устойчивости представляют значительные трудности, поэтому в условиях эксплуатации окончательное решение вопросов обеспечения результирующей устойчивости следует принимать, как правило, на основе натурных испытаний.